【题目】如图,矩形OABC的边OA,OC分别在x轴、y轴上,点B在第一象限,点D在边BC上,且∠AOD=30°,四边形OA′B′D与四边形OABD关于直线OD对称(点A′和A,B′和B分别对应).若AB=1,反比例函数y= ![]() (k≠0)的图象恰好经过点A′,B,则k的值为 .
(k≠0)的图象恰好经过点A′,B,则k的值为 . 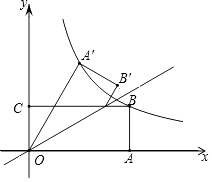
参考答案:
【答案】![]()
【解析】解:∵四边形ABCO是矩形,AB=1,
∴设B(m,1),
∴OA=BC=m,
∵四边形OA′B′D与四边形OABD关于直线OD对称,
∴OA′=OA=m,∠A′OD=∠AOD=30°,
∴∠A′OA=60°,
过A′作A′E⊥OA于E,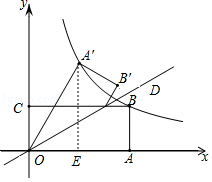
∴OE= ![]() m,A′E=
m,A′E= ![]() m,
m,
∴A′( ![]() m,
m, ![]() m),
m),
∵反比例函数y= ![]() (k≠0)的图象恰好经过点A′,B,
(k≠0)的图象恰好经过点A′,B,
∴ ![]() m
m ![]() m=m,
m=m,
∴m= ![]() ,
,
∴k= ![]() .
.
所以答案是: ![]() .
.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
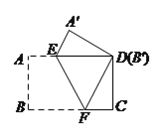
查看答案和解析>>【题目】把一张长方形纸片按如图方式折叠,使顶点
 和点
和点 重合,折痕为
重合,折痕为 .若
.若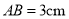 ,
, 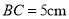 .
.
求(
 )
) 的长.
的长.(
 )重叠部分
)重叠部分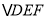 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1所示∠AOB的纸片,OC平分∠AOB,如图2把∠AOB沿OC对折成∠COB(OA与OB重合),从O点引一条射线OE,使∠BOE=
 ∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.
∠EOC,再沿OE把角剪开,若剪开后得到的3个角中最大的一个角为76°,则∠AOB=_____________°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一次“构造勾股数”的探究性学习中,老师给出了下表:
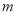
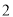
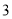
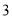
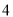
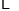
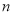
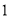
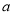
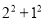
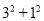
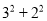
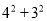
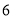
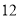
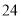
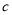
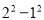
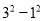
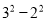
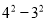
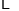
其中
 、
、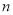 为正整数,且
为正整数,且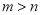 .
.(
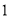 )观察表格,当
)观察表格,当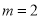 ,
, 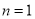 时,此时对应的
时,此时对应的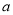 、
、 、
、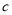 的值能否为直角三角形三边的长?说明你的理由.
的值能否为直角三角形三边的长?说明你的理由.(
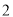 )探究
)探究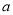 ,
, 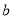 ,
, 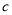 与
与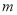 、
、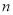 之间的关系并用含
之间的关系并用含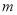 、
、 的代数式表示:
的代数式表示: 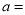 __________,
__________, 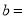 __________,
__________,  __________.
__________.(
 )以
)以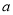 ,
, 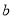 ,
, 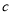 为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例.
为边长的三角形是否一定为直角三角形?如果是,请说明理由;如果不是,请举出反例. -
科目: 来源: 题型:
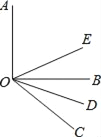
查看答案和解析>>【题目】如图所示,OE,OD分别平分∠AOC和∠BOC,
(1)如果∠AOB=90°,∠BOC=38°,求∠DOE的度数;
(2)如果∠AOB=α,∠BOC=β(α、β均为锐角,α>β),其他条件不变,求∠DOE;
(3)从(1)、(2)的结果中,你发现了什么规律,请写出来.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明学了有理数的乘方后,知道23=8,25=32,他问老师,有没有20,2﹣3,如果有,等于多少?老师耐心提示他:25÷23=4,25﹣3=4,即25÷23=25﹣3=22=4,…“哦,我明白了了,”小明说,并且很快算出了答案,亲爱的同学,你想出来了吗?
(1)请仿照老师的方法,推算出20,2﹣3的值.
(2)据此比较(﹣3)﹣2与(﹣2)﹣3的大小.(写出计算过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列材料,然后解答问题.
探究:用的幂的形式表示aman的结果(m、为正整数).
根据乘方的意义,aman=
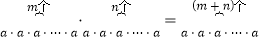 =am+n.
=am+n.(1)请根据以上结论填空:36×38= ,52×53×57= ,(a+b)3(a+b)5= ;
(2)仿照以上的分析过程,用的幂的形式表示(am)n的结果(提示:将am看成一个整体).
相关试题

