【题目】我国古籍《周髀算经》中早有记载“勾三股四弦五”,下面我们来探究两类特殊的勾股数.通过观察完成下面两个表格中的空格(以下a、b、c为Rt△ABC的三边,且a<b<c):
表一 表二
a | b | c | a | b | c | |
3 | 4 | 5 | 6 | 8 | 10 | |
5 | 12 | 13 | 8 | 15 | 17 | |
7 | 24 | 25 | 10 | 24 | 26 | |
9 | 41 | 12 | 37 |
(1)仔细观察,表一中a为大于1的奇数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(2)仔细观察,表二中a为大于4的偶数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(3)我们还发现,表一中的三边长“3,4,5”与表二中的“6,8,10”成倍数关系,表一中的“5,12,13”与表二中的“10,24,26”恰好也成倍数关系……请直接利用这一规律计算:在Rt△ABC中,当![]() ,
,![]() 时,斜边c的值.
时,斜边c的值.
参考答案:
【答案】 b+1=c a2=b+c b+2=c a2=2(b+c)
【解析】分析:(1)根据图表中数据结合勾股定理得出即可;
(2)利用图表中数据即可得出b、c的数量关系;
(3)利用图表中数据即可得出b、a的数量关系;
(4)利用勾股定理得出即可.
详解:(1)如图所示:
表一 表二
a | b | c | a | b | c | |
3 | 4 | 5 | 6 | 8 | 10 | |
5 | 12 | 13 | 8 | 15 | 17 | |
7 | 24 | 25 | 10 | 24 | 26 | |
9 | 40 | 41 | 12 | 35 | 37 |
(2)根据表格数据可得:
表一中a为大于l的奇数,此时b、c的数量关系是b+1=c;a、b、c之间的数量关系是a2=b+c
表二中a为大于4的偶数,此时b、c的数量关系是b+2=c;a、b、c之间的数量关系是a2=2(b+c)
(3)∵![]() ,∴
,∴![]() ,∴c=1.
,∴c=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A在⊙O上,点P是⊙O外一点,PA切⊙O于点A,连接OP交⊙O于点D,作AB⊥OP于点C,交⊙O于点B,连接PB.

(1)求证:PB是⊙O的切线;
(2)若PC=9,AB=6 , ①求图中阴影部分的面积;
, ①求图中阴影部分的面积; -
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)问题背景
如图①,BC是⊙O的直径,点A在⊙O上,AB=AC,P为BmC上一动点(不与B,C重合),求证: PA=PB+PC.
PA=PB+PC.
小明同学观察到图中自点A出发有三条线段AB,AP,AC,且AB=AC,这就为旋转作了铺垫.于是,小明同学有如下思考过程:
第一步:将△PAC绕着点A顺时针旋转90°至△QAB(如图①);
第二步:证明Q,B,P三点共线,进而原题得证.
请你根据小明同学的思考过程完成证明过程.
(2)类比迁移
如图②,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=AC,AB⊥AC,垂足为A,求OC的最小值.
(3)拓展延伸
如图③,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB= AC,AB⊥AC,垂足为A,则OC的最小值为 .
AC,AB⊥AC,垂足为A,则OC的最小值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子里有完全相同的三个小球,球上分别标有数字﹣2,1,4.随机摸出一个小球(不放回),其数字为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
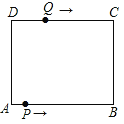
查看答案和解析>>【题目】如图在长方形ABCD中,AB=12cm,BC=8cm,点P从A点出发,沿A→B→C→D路线运动,到D点停止;点Q从D点出发,沿D→C→B→A运动,到A点停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,用x(秒)表示运动时间.
(1)求点P和点Q相遇时的x值.
(2)连接PQ,当PQ平分矩形ABCD的面积时,求运动时间x值.
(3)若点P、点Q运动到6秒时同时改变速度,点P的速度变为每秒3cm,点Q的速度为每秒1cm,求在整个运动过程中,点P、点Q在运动路线上相距路程为20cm时运动时间x值.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的对角线相交于点O,∠CAB的平分线分别交BD、BC于E、F,作BH⊥AF于点H,分别交AC、CD于点G、P,连结GE、GF.
(1)求证:△OAE≌△OBG.
(2)试问:四边形BFGE是否为菱形?若是,请证明;若不是,请说明理由.

-
科目: 来源: 题型:
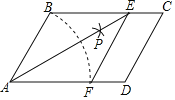
查看答案和解析>>【题目】如图,在□ABCD中,以点A为圆心,AB长为半径画弧交AD于点F,再分别以点B、F为圆心,以大于
 BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,得四边形ABEF.
BF的相同长为半径画弧,两弧交于点P;连接AP并延长交BC于点E,连接EF,得四边形ABEF. 求证:四边形ABEF是菱形.
相关试题

