【题目】如图,点A在⊙O上,点P是⊙O外一点,PA切⊙O于点A,连接OP交⊙O于点D,作AB⊥OP于点C,交⊙O于点B,连接PB. 
(1)求证:PB是⊙O的切线;
(2)若PC=9,AB=6 ![]() , ①求图中阴影部分的面积;
, ①求图中阴影部分的面积;
参考答案:
【答案】
(1)证明:如图1,连接OB,
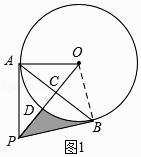
∵OP⊥AB,OP经过圆心O,
∴AC=BC,
∴OP垂直平分AB,
∴AP=BP,
∵OA=OB,OP=OP,
∴△APO≌△BPO(SSS),
∴∠PAO=∠PBO,
∵PA切⊙O于点A,
∴AP⊥OA,
∴∠PAO=90°,
∴∠PBO=∠PAO=90°,
∴OB⊥BP,
又∵点B在⊙O上,
∴PB与⊙O相切于点B;
(2)解:如图1,

∵OP⊥AB,OP经过圆心O,
∴BC= ![]() AB=3
AB=3 ![]() ,
,
∵∠PBO=∠BCO=90°,
∴∠PBC+∠OBC=∠OBC+∠BOC=90°,
∴∠PBC=∠BOC,
∴△PBC∽△BOC,
∴ ![]()
∴OC= ![]() =
= ![]() =3,
=3,
∴在Rt△OCB中,OB= ![]() =
= ![]() =6,tan∠COB=
=6,tan∠COB= ![]() =
= ![]() ,
,
∴∠COB=60°,
∴S△OPB= ![]() ×OP×BC=
×OP×BC= ![]() ×
× ![]() =18
=18 ![]() ,S扇DOB=
,S扇DOB= ![]() =6π,
=6π,
∴S阴影=S△OPB﹣S扇DOB=18 ![]() ﹣6π;
﹣6π;
②若点E是⊙O上一点,连接AE,BE,当AE=6 ![]() 时,BE= .
时,BE= .
3 ![]() ﹣3
﹣3 ![]() 或3
或3 ![]() +3
+3 ![]()
【解析】②分两种情况: i)当点E在 ![]() 上时,如图2,作直径AF,交⊙O于F,连接EF、EB,过O作OG⊥AE于G,过F作FH⊥EB于H,
上时,如图2,作直径AF,交⊙O于F,连接EF、EB,过O作OG⊥AE于G,过F作FH⊥EB于H,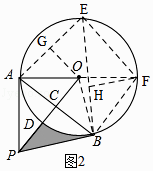
∴EG=AG= ![]() AE=
AE= ![]() ×
× ![]() =3
=3 ![]() ,
,
∵∠AOB=120°,OA=OB,
∴∠OAB=30°,
∴∠BEF=∠OAB=30°,
Rt△OGE中,由①知:OA=6,
∴OG= ![]() =
= ![]() =3
=3 ![]() ,
,
∴AG=OG,
∴△OGA是等腰直角三角形,
∴∠OAE=45°,
∴∠EBF=∠OAE=45°,
∵AF是⊙O的直径,
∴∠AEF=90°,
∴△AEF是等腰直角三角形,
∴EF=AE=6 ![]() ,
,
Rt△EHF中,∠BEF=30°,
∴FH= ![]() EF=3
EF=3 ![]() ,
,
∴EH= ![]() =
= ![]() =3
=3 ![]() ,
,
Rt△BHF中,∵∠EBF=45°,
∴△BHF是等腰直角三角形,
∴BH=FH=3 ![]() ,
,
∴BE=3 ![]() +3
+3 ![]() ,
,
ii)当点E在劣弧 ![]() 上时,如图3,
上时,如图3,
作直径AF,并⊙O于F,连接OB、OE、BF,过B作BH⊥OE于H,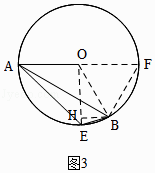
∵AF为⊙O的直径,
∴∠ABF=90°,
∵∠BAF=30°,
∴∠F=∠BOF=60°,
∵OA=OE=6,AE=6 ![]() ,
,
∴OA2+OE2=AE2 ,
∴∠AOE=90°,
∴∠EOF=90°,
∴∠EOB=30°,
Rt△OHB中,BH= ![]() OB=3,
OB=3,
∴OH= ![]() =3
=3 ![]() ,
,
∴EH=6﹣3 ![]() ,
,
∴BE= ![]() =
= ![]() =
= ![]() =3
=3 ![]() ﹣3
﹣3 ![]() ;
;
综上所述,BE的长为3 ![]() +3
+3 ![]() 或3
或3 ![]() ﹣3
﹣3 ![]() ;
;
所以答案是:3 ![]() ﹣3
﹣3 ![]() 或3
或3 ![]() +3
+3 ![]() .
.
【考点精析】通过灵活运用垂径定理和扇形面积计算公式,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2)即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣(a﹣1)x+a﹣2,其中a是常数.
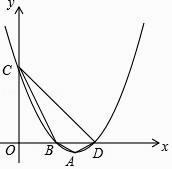
(1)求证:不论a为何值,该二次函数的图象与x轴一定有公共点;
(2)当a=4时,该二次函数的图象顶点为A,与x轴交于B,D两点,与y轴交于C点,求四边形ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】生态公园计划在园内的坡地上种植一片有A、B两种树的混合林,需要购买这两种树苗共100棵.假设这批树苗种植后成活95棵,种植A、B两种树苗的相关信息如下表:

(1)求购买这两种树苗各多少棵?
(2)求种植这片混合林的总费用需多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在一条笔直的公路上有M、P、N三个地点,M、P两地相距20km,甲开汽车,乙骑自行车分别从M、P两地同时出发,匀速前往N地,到达N地后停止运动.已知乙骑自行车的速度为20km/h,甲,乙两人之间的距离y(km)与乙行驶的时间t(h)之间的关系如图②所示.

(1)M、N两地之间的距离为km;
(2)求线段BC所表示的y与t之间的函数表达式;
(3)若乙到达N地后,甲,乙立即以各自原速度返回M地,请在图②所给的直角坐标系中补全函数图象. -
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)问题背景
如图①,BC是⊙O的直径,点A在⊙O上,AB=AC,P为BmC上一动点(不与B,C重合),求证: PA=PB+PC.
PA=PB+PC.
小明同学观察到图中自点A出发有三条线段AB,AP,AC,且AB=AC,这就为旋转作了铺垫.于是,小明同学有如下思考过程:
第一步:将△PAC绕着点A顺时针旋转90°至△QAB(如图①);
第二步:证明Q,B,P三点共线,进而原题得证.
请你根据小明同学的思考过程完成证明过程.
(2)类比迁移
如图②,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=AC,AB⊥AC,垂足为A,求OC的最小值.
(3)拓展延伸
如图③,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB= AC,AB⊥AC,垂足为A,则OC的最小值为 .
AC,AB⊥AC,垂足为A,则OC的最小值为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个盒子里有完全相同的三个小球,球上分别标有数字﹣2,1,4.随机摸出一个小球(不放回),其数字为p,再随机摸出另一个小球其数字记为q,则满足关于x的方程x2+px+q=0有实数根的概率是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国古籍《周髀算经》中早有记载“勾三股四弦五”,下面我们来探究两类特殊的勾股数.通过观察完成下面两个表格中的空格(以下a、b、c为Rt△ABC的三边,且a<b<c):
表一 表二
a
b
c
a
b
c
3
4
5
6
8
10
5
12
13
8
15
17
7
24
25
10
24
26
9
41
12
37
(1)仔细观察,表一中a为大于1的奇数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(2)仔细观察,表二中a为大于4的偶数,此时b、c的数量关系是_____________,
a、b、c之间的数量关系是_________________________;
(3)我们还发现,表一中的三边长“3,4,5”与表二中的“6,8,10”成倍数关系,表一中的“5,12,13”与表二中的“10,24,26”恰好也成倍数关系……请直接利用这一规律计算:在Rt△ABC中,当
 ,
, 时,斜边c的值.
时,斜边c的值.
相关试题

