【题目】解方程:
(1)3(20-y)=6y-4(y-11);
(2)![]()
参考答案:
【答案】(1)y=3.2;(2)x=![]() .
.
【解析】
试题(1)按照去括号,移项,合并同类项,系数化为1的步骤解答,去括号时一是不要漏乘括号内的项,二是明确括号前的符号;(2)按照去分母,去括号,移项,合并同类项,系数化为1的步骤解答,去分母一要注意不要漏乘没有分母的项,二要注意去掉分母后把分子加括号.
(1) 3(20 - y)= 6 y- 4(y-11)
去括号得, 60 – 3 y =6 y- 4y + 44
移项得, - 3 y- 2 y=44-60
合并得, -5 y = - 16
系数化为1得, y=3.2
(2)![]()
去分母得,6-(x-1)=2(3x-1),
去括号得, 6-x+1=6x-2,
移项得, -x-6x=-2-6-1,
合并得, -7x=-9
化系数为1得, x=![]() .
.
-
科目: 来源: 题型:
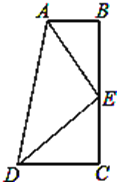
查看答案和解析>>【题目】如图,∠B=∠C=90°,E是BC的中点,DE平分∠ADC.
(1)求证:AE是∠DAB的平分线;
(2)探究:线段AD、AB、CD之间有何数量关系?请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(探索新知)
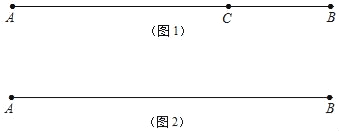
如图1,点C在线段AB上,图中共有3条线段:AB、AC和BC,若其中有一条线段的长度是另一条线段长度的两倍,则称点C是线段AB的“二倍点”.
(1)一条线段的中点 这条线段的“二倍点”;(填“是”或“不是”)
(深入研究)
如图2,若线段AB=20cm,点M从点B的位置开始,以每秒2cm的速度向点A运动,当点M到达点A时停止运动,运动的时间为t秒.
(2)问t为何值时,点M是线段AB的“二倍点”;
(3)同时点N从点A的位置开始,以每秒1cm的速度向点B运动,并与点M同时停止.请直接写出点M是线段AN的“二倍点”时t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)25×26=________;
(2)
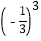 ×
×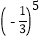 =________;
=________;(3)-a2·a5=________;
(4)x2·x2m-2=________;
(5)(-b)2·(-b)3·(-b)5=________;
(6)x·x4+x5=________.
-
科目: 来源: 题型:
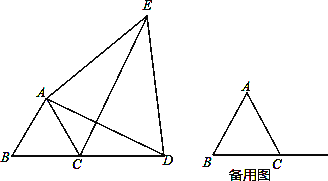
查看答案和解析>>【题目】如图,已知△ABC为等边三角形,点D由点C出发,在BC的延长线上运动,连结AD,以AD为边作等边三角形ADE,连结CE.
(1)请写出AC、CD、CE之间的数量关系,并证明;
(2)若AB=6cm,点D的运动速度为每秒2cm,运动时间为t秒,则t为何值时,CE⊥AD?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
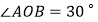 ,在射线
,在射线 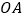 上取点
上取点 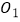 ,以
,以 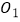 为圆心的圆与
为圆心的圆与 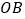 相切;在射线
相切;在射线  上取点
上取点 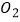 ,以
,以 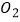 为圆心,
为圆心, 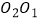 为半径的圆与
为半径的圆与 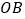 相切;在射线
相切;在射线 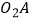 上取点
上取点 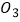 ,以
,以 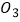 为圆心,
为圆心, 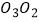 为半径的圆与
为半径的圆与 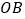 相切;
相切;  ;在射线
;在射线 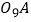 上取点
上取点 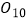 ,以
,以 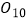 为圆心,
为圆心,  为半径的圆与
为半径的圆与 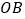 相切.若
相切.若 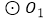 的半径为
的半径为  ,则
,则 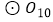 的半径长是 .
的半径长是 . 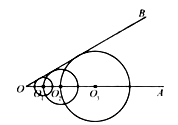
相关试题

