【题目】小明在没有量角器和圆规的情况下,利用刻度尺和一副三角板画出了一个角的平分线,他的做法是这样的:如图.
(1)在![]() 的内部任取一个点E,过点E作EM⊥OB;
的内部任取一个点E,过点E作EM⊥OB;
(2)在边![]() 上取一点N,作NF⊥OA于点N,且NF=EM;
上取一点N,作NF⊥OA于点N,且NF=EM;
(3)过点E作直线l1∥OB,过点F作直线l2∥OA,l1 与l2交于点![]() ;
;
(4)画射线![]() .
.
则射线![]() 为
为![]() 的平分线.
的平分线.

根据小明的画法回答下面的问题:
(1)小明作l1∥OB,l2∥OA的目的是___________________________________________;
(2)l1 与l2交于点![]() ,则射线
,则射线![]() 为
为![]() 的平分线的依据是__________________________.
的平分线的依据是__________________________.
参考答案:
【答案】利用平行线间的距离处处相等 到角两边距离相等的点在角的平分线上.
【解析】
(1)作l1∥OB,l2∥OA的目的是:利用平行线间的距离处处相等;
(2)过点P作PG⊥OA于G,PH⊥OB于H,再根据l1∥OB,EM⊥OB得出PH= EM;再根据 l2∥OA,NF⊥OA,得出PG=FN,再根据NF=EM,得出PG=PH,根据到角两边距离相等的点在角的平分线上,从而得出射线![]() 为
为![]() 的平分线.
的平分线.
(1)作l1∥OB,l2∥OA的目的是利用平行线间的距离处处相等;
故答案为: 利用平行线间的距离处处相等;
(2)过点P作PG⊥OA于G,PH⊥OB于H,
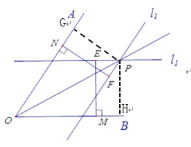
∵l1∥OB,EM⊥OB,∴PH= EM;
∵l2∥OA,NF⊥OA, ∴PG=FN
∵NF=EM,∴PG=PH,
∴射线![]() 为
为![]() 的平分线(到角两边距离相等的点在角的平分线上).
的平分线(到角两边距离相等的点在角的平分线上).
故答案为: 到角两边距离相等的点在角的平分线上.
-
科目: 来源: 题型:
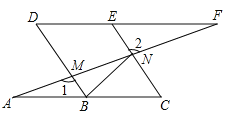
查看答案和解析>>【题目】如图,点B、E分别在AC、DF上,AF分别交BD、CE于点M、N,∠A=∠F,∠1=∠2.
(1)求证:四边形BCED是平行四边形;
(2)已知DE=2,连接BN,若BN平分∠DBC,求CN的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长AB=4,分别以点A、B为圆心,AB长为半径画弧,两弧交于点E,则
 的长是( )
的长是( )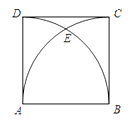
A.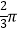
B.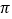
C.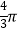
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】水果商贩老徐上水果批发市场进货,他了解到草莓的批发价格是每箱60元,苹果的批发价格是每箱40元.老徐购得草莓和苹果共60箱,刚好花费3100元.
(1)问草莓、苹果各购买了多少箱?
(2)老徐有甲、乙两家店铺,每售出一箱草莓或苹果,甲店分别获利15元和20元,乙店分别获利12元和16元.设老徐将购进的60箱水果分配给甲店草莓
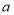 箱,苹果
箱,苹果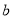 箱,其余均分配给乙店.由于他口碑良好,两家店都很快卖完了这批水果.
箱,其余均分配给乙店.由于他口碑良好,两家店都很快卖完了这批水果.①若老徐在甲店获利600元,则他在乙店获利多少元?
②若老徐希望获得总利润为1000元,则
 =_______.(直接写出答案)
=_______.(直接写出答案) -
科目: 来源: 题型:
查看答案和解析>>【题目】(理解新知)
如图①,已知
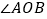 ,在
,在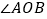 内部画射线
内部画射线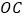 ,得到三个角,分别为
,得到三个角,分别为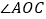 、
、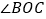 、
、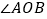 ,若这三个角中有一个角是另外一个角的2倍,则称射线
,若这三个角中有一个角是另外一个角的2倍,则称射线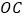 为
为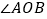 的“2倍角线”
的“2倍角线”(1)角的平分线 这个角的“2倍角线”;(填“是”或“不是”)
(2)若
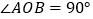 ,射线
,射线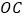 为
为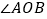 的“2倍角线”,则
的“2倍角线”,则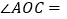
 ;
;(解决问题)
如图②,已知
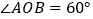 ,射线
,射线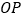 从
从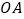 出发,以每秒
出发,以每秒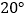 的速度绕
的速度绕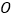 点逆时针旋转:射线
点逆时针旋转:射线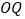 从
从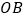 出发,以每秒
出发,以每秒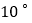 的速度绕
的速度绕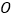 点顺时针旋转,射线
点顺时针旋转,射线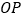 、
、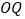 同时出发,当一条射线回到出发位置的时候,整个运动随之停止.设运动的时间为
同时出发,当一条射线回到出发位置的时候,整个运动随之停止.设运动的时间为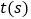 .
.(3)当射线
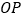 、
、 旋转到同一条直线上时,求
旋转到同一条直线上时,求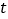 的值;
的值;(4)若
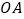 、
、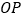 、
、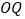 三条射线中,一条射线恰好是以另外两条射线为边的角的“2倍角线”,直接写出所有可能的
三条射线中,一条射线恰好是以另外两条射线为边的角的“2倍角线”,直接写出所有可能的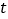 的值.(本题中所研究的角都是小于等于
的值.(本题中所研究的角都是小于等于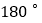 的角.)
的角.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A的坐标为(0,3),点B和点D的坐标分别为(m,0),(n,4),且m>0,四边形ABCD是矩形.
(1)如图1,当四边形ABCD为正方形时,求m,n的值;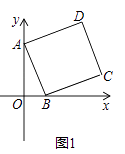
(2)在图2中,画出矩形ABCD,简要说明点C,D的位置是如何确定的,并直接用含m的代数式表示点C的坐标;
(3)探究:当m为何值时,矩形ABCD的对角线AC的长度最短. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A、B、C是不在同一条直线上的三点,请按下列要求画图并作答(画图时工具不限,不需写出结论,只需画出图形、标注字母):
(1)画直线BC,连接AC;
(2)画线段BC的中点D,连接AD;
(3)画出∠ADC的平分线交AC于点E;
(4)若∠BDA=
 求∠ADC,∠EDC.
求∠ADC,∠EDC.
相关试题

