【题目】已知:如图,在等腰梯形ABCD中,AD//BC,∠BDC=∠BCD,点E是线段BD上一点,且BE=AD. 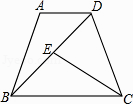
(1)证明:△ADB≌△EBC;
(2)直接写出图中所有的等腰三角形.
参考答案:
【答案】
(1)证明:∵AD//BC,
∴∠ADB=∠EBC,
∵∠BDC=∠BCD,
∴BD=BC,
在△ADB和△EBC中,

∴△ADB≌△EBC(SAS)
(2)解:由(1)可得△BCD是等腰三角形;
∵△ADB≌△EBC,
∴CE=AB,
又∵AB=CD,
∴CE=CD,
∴△CDE是等腰三角形
【解析】(1)根据平行线的性质判定∠ADB=∠EBC,然后由∠BDC=∠BCD,得出BD=BC,结合BE=AD,利用SAS可证明结论;(2)根据(1)的结论,可得CE=AB,结合等腰梯形的性质,可写出等腰三角形.
【考点精析】关于本题考查的等腰三角形的判定和等腰梯形的性质,需要了解如果一个三角形有两个角相等,那么这两个角所对的边也相等(简称:等角对等边).这个判定定理常用于证明同一个三角形中的边相等;等腰梯形的两腰相等;同一底上的两个角相等;两条对角线相等才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答题
(1)先化简,再求值:1﹣ ]÷
]÷  +
+  ,其中a=
,其中a=  .
.
(2)解不等式组: .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知数轴上的点A表示的数为6,点B表示的数为﹣4,点C到点A、点B的距离相等,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为x(x大于0)秒.
(1)点C表示的数是 ;
(2)当x= 秒时,点P到达点A处?
(3)运动过程中点P表示的数是 (用含字母x的式子表示);
(4)当P,C之间的距离为2个单位长度时,求x的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小兵、小颖三人的家和学校在同一条东西走向的路上,星期天,老师到这三家进行家访,从学校出发先向东走 250m 到小明家,后又向东走 350m 到小兵家,再向西行 800m 到小颖家,最后回到学校.
(1)以学校为原点,画出数轴并在数轴上分别表示出小明、小兵、小颖家的位置;
(2)小明家距离小颖家多远?
(3)这次家访,老师共走了多少千米的路程?
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇准备完成题目:化简:
 ,发现系数“
,发现系数“ ”印刷不清楚.
”印刷不清楚.(1)他把“
 ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“
 ”是几?
”是几? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M,N分别是AC,BC的中点.
(1)求线段MN的长.
(2)若C为线段AB上任一点,满足AC+CB=a cm,其他条件不变,你能猜想MN的长度吗?(用含a的代数式表示)并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知一次函数y=﹣
 x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )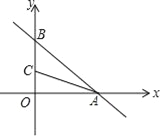
A. (0,3) B. (0,
 ) C. (0,
) C. (0, ) D. (0,
) D. (0, )
)
相关试题

