【题目】如图,点C在线段AB上,AC=8 cm,CB=6 cm,点M,N分别是AC,BC的中点.
(1)求线段MN的长.
(2)若C为线段AB上任一点,满足AC+CB=a cm,其他条件不变,你能猜想MN的长度吗?(用含a的代数式表示)并说明理由.
![]()
参考答案:
【答案】(1) 7(cm); (2) ![]() a cm.
a cm.
【解析】试题分析:(1)根据M、N分别是AC、BC的中点,我们可得出MC、NC分别是AC、BC的一半,那么MC、CN的和就应该是AC、BC和的一半,也就是说MN是AB的一半,有了AC、CB的值,那么就有了AB的值,也就能求出MN的值了;
(2)根据线段中点的性质,可得MC=![]() AC,NC=
AC,NC=![]() BC,根据线段的和差,可得答案.
BC,根据线段的和差,可得答案.
试题解析:(1)因为点M,N分别是AC,BC的中点,
所以CM=![]() AC=
AC=![]() ×8=4(cm),CN=
×8=4(cm),CN=![]() BC=
BC=![]() ×6=3(cm),
×6=3(cm),
所以MN=CM+CN=4+3=7(cm);
(2)MN=![]() acm.理由如下:
acm.理由如下:
同(1)可得CM=![]() AC,CN=
AC,CN=![]() BC,
BC,
所以MN=CM+CN=![]() AC+
AC+![]() BC=
BC=![]() (AC+BC)=
(AC+BC)= ![]() a(cm).
a(cm).
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明、小兵、小颖三人的家和学校在同一条东西走向的路上,星期天,老师到这三家进行家访,从学校出发先向东走 250m 到小明家,后又向东走 350m 到小兵家,再向西行 800m 到小颖家,最后回到学校.
(1)以学校为原点,画出数轴并在数轴上分别表示出小明、小兵、小颖家的位置;
(2)小明家距离小颖家多远?
(3)这次家访,老师共走了多少千米的路程?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在等腰梯形ABCD中,AD//BC,∠BDC=∠BCD,点E是线段BD上一点,且BE=AD.
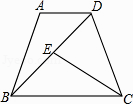
(1)证明:△ADB≌△EBC;
(2)直接写出图中所有的等腰三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇准备完成题目:化简:
 ,发现系数“
,发现系数“ ”印刷不清楚.
”印刷不清楚.(1)他把“
 ”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);
”猜成3,请你化简:(3x2+6x+8)–(6x+5x2+2);(2)他妈妈说:“你猜错了,我看到该题标准答案的结果是常数.”通过计算说明原题中“
 ”是几?
”是几? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,已知一次函数y=﹣
 x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )
x+6与x,y轴分别交于A,B两点,点C(0,n)是y轴上一点,把坐标平面沿直线AC折叠,点B刚好落在x轴上,则点C的坐标是( )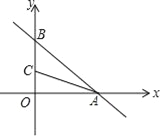
A. (0,3) B. (0,
 ) C. (0,
) C. (0, ) D. (0,
) D. (0, )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】为降低空气污染,公交公司决定全部更换节能环保的燃气公交车.计划购买A型和B型两种公交车共10辆,其中每台的价格,年均载客量如表:
A型
B型
价格(万元/辆)
a
b
年均载客量(万人/年/辆)
60
100
若购买A型公交车1辆,B型公交车2辆,共需400万元;若购买A型公交车2辆,B型公交车1辆,共需350万元
(1)求购买每辆A型公交车和每辆B型公交车分别多少万元?
(2)如果该公司购买A型和B型公交车的总费用不超过1200万元,且确保这10辆公交车年均载客总和不少于680万人次,有哪几种购车方案?请你设计一个方案,使得购车总费用最少. -
科目: 来源: 题型:
查看答案和解析>>【题目】“农民也可以报销医疗费了!”这是某市推行新型农村医疗合作的成果.村民只要每人每年交10元钱,就可以加入合作医疗,每年先由自己支付医疗费,年终时可得到按一定比例返回的返回款.这一举措极大地增强了农民抵御大病风险的能力.小华与同学随机调查了他们乡的一些农民,根据收集到的数据绘制了以下的统计图.

根据以上信息,解答以下问题:
(1)本次调查了多少村民,被调查的村民中,有多少人参加合作医疗得到了返回款;
(2)该乡若有10 000村民,请你估计有多少人参加了合作医疗?要使两年后参加合作医疗的人数增加到9 680人,假设这两年的年增长率相同,求这个年增长率.
相关试题

