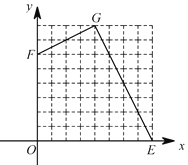
【题目】如图,在平面直角坐标系 ![]() 中,
中,![]() ,
,![]() .
.
①当 ![]() 时,则
时,则![]() ______;
______;
②在图中的网格区域内找一点![]() ,使
,使![]() ,且四边形
,且四边形![]() 被过
被过![]() 点的一条直线分割成两部分后,可以拼成一个正方形,则
点的一条直线分割成两部分后,可以拼成一个正方形,则![]() 点坐标为_______.
点坐标为_______.
参考答案:
【答案】![]()
![]()
【解析】
(1)先利用勾股定理分别计算三边长,再利用勾股定理的逆定理可得:∠FGE=90°;
(2)构建全等三角形:△APF≌△MEP,构建P的位置,根据三角形全等得到正方形.
(1)如图1,连接EF,
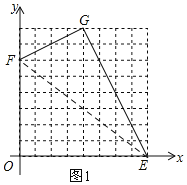
由勾股定理得:FG2=22+42=20,
GE2=42+82=80,
EF2=62+82=100,
∴FG2+GE2=EF2,
∴∠FGE=90°,
故答案为:90°;
(2)如图2,过P作PM⊥x轴于M,当P(7,7),PM为分割线;
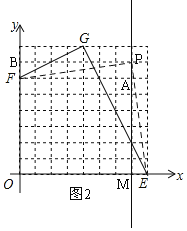
根据格点的长度易得:△APF≌△MEP≌△BFP,
∴∠APF=∠MEP,
∵∠MEP+∠MPE=90°,
∴∠APF+∠MPE=90°,
即∠FPE=90°,
四边形OEPF将△EPM剪下放在△BFP上,构建正方形BOMP;
故答案为:(7,7).
-
科目: 来源: 题型:
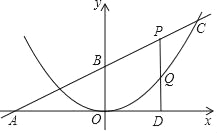
查看答案和解析>>【题目】如图,直线y=kx+b与坐标轴交于A,B两点,其中点B的坐标为(0,4),tan∠BAO=
 ,一条抛物线的顶点为坐标原点,且与直线y=kx+b交于点C(m,8),点P为线段BC上一动点(不与点B,点C重合),PD⊥x轴于点D,交抛物线于点Q.
,一条抛物线的顶点为坐标原点,且与直线y=kx+b交于点C(m,8),点P为线段BC上一动点(不与点B,点C重合),PD⊥x轴于点D,交抛物线于点Q.(1)求直线和抛物线的函数关系式;
(2)设点P的横坐标为t,线段PQ的长度为d,求出d与t之间的函数关系式,并求出d的最大值;
(3)是否存在点P的位置,使得以点P,D,B为顶点的三角形是等腰三角形?如果存在,直接写出点P的坐标;如果不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料,并解决后面的问题.
材料:一般地,
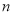 个相同的因数
个相同的因数 相乘:
相乘: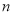 个
个 记为
记为 ,如
,如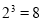 ,此时,3叫做以2为底8的对数,记为
,此时,3叫做以2为底8的对数,记为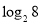 (即
(即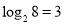 ).
).一般地,若
 (
(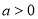 且
且 ,
,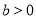 ),则
),则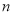 叫做以
叫做以 为底
为底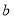 的对数,记为
的对数,记为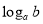 (即
(即 ).如
).如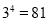 ,则4叫做以3为底81的对数,记为
,则4叫做以3为底81的对数,记为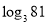 (即
(即 ).
).问题:(1)计算以下各对数的值:
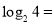 ________,
________, ________,
________, ________.
________.(2)观察(1)中三数4、16、64之间满足怎样的关系式?
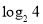 、
、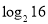 、
、 之间又满足怎样的关系式?______________________________________________________________________________
之间又满足怎样的关系式?______________________________________________________________________________(3)由(2)的结果,你能归纳出一个一般性的结论吗?
 ____________________(
____________________(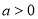 且
且 ,
,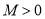 ,
, )
)(4)根据幂的运算法则:
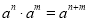 以及对数的含义证明(3)中结论.
以及对数的含义证明(3)中结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】推理填空:
如图,
 ,
, ,将说明
,将说明 成立的理由填写完整.
成立的理由填写完整.
解:因为
 (已知),
(已知),所以
 (________________)
(________________)又因为
 (已知),
(已知),所以
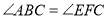 (等量代换),
(等量代换),所以________________(同位角相等,两直线平行),
所以
 (________________________________)
(________________________________) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,Rt△ABC的直角边AB在x轴上,∠ABC=90°.点A的坐标为(1,0),点C的坐标为(3,4),M是BC边的中点,函数
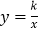 (
( )的图象经过点M.
)的图象经过点M. (1)求k的值;
(2)将△ABC绕某个点旋转180°后得到△DEF(点A,B,C的对应点分别为点D,E,F),且EF在y轴上,点D在函数
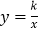 (
( )的图象上,求直线DF的表达式.
)的图象上,求直线DF的表达式.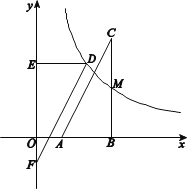
-
科目: 来源: 题型:
查看答案和解析>>【题目】旅游公司在景区内配置了50辆观光车共游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x(元)是5的倍数.发现每天的营运规律如下:当x不超过100元时,观光车能全部租出;当x超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆.已知所有观光车每天的管理费是1100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入﹣管理费)
(2)当每辆车的日租金为多少元时,每天的净收入最多?
-
科目: 来源: 题型:
查看答案和解析>>【题目】小马虎解方理
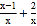 =3出现了错误,解答过程如下:
=3出现了错误,解答过程如下:方程两边都乘以x,得x﹣1+2=3(第一步)
移项,合并同类项,得x=2(第二步)
经检验,x=2是原方程的解(第三步)
(1)小马虎解答过程是从第 步开始出错的,出错原因是 ;
(2)请写出此题正确的解答过程.
相关试题

