【题目】如图,正方形ABCD中,以对角线BD为边作菱形BDFE,使B,C,E三点在同一直线上,连接BF,交CD与点G. 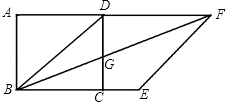
(1)求证:CG=CE;
(2)若正方形边长为4,求菱形BDFE的面积.
参考答案:
【答案】
(1)解:连接DE,

则DE⊥BF,
∵∠ODG+∠OGD=90°,∠CBG+∠CGB=90°,∠CGB=∠OGD
∴∠CDE=∠CBG,
又∵BC=DC,∠BCG=∠DCE,
∴△BCG≌△DCE(ASA),
∴CG=CE,
(2)解:正方形边长BC=4,则BD= ![]() BC=4
BC=4 ![]() ,
,
菱形BDFE的面积为S=4 ![]() ×4=16
×4=16 ![]() .
.
答:菱形BDFE的面积为16 ![]()
【解析】(1)连接DE,则DE⊥BF,可得∠CDE=∠CBG,根据BC=DC,∠BCG=∠DCE,可证△BCG≌△DCE,可证CG=CE;(2)已知正方形的边长可以证明BD,即BE,根据BE,DC即可求菱形BDFE的面积.
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.
-
科目: 来源: 题型:
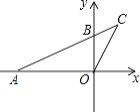
查看答案和解析>>【题目】如图,在直角坐标系xOy中,A(﹣4,0),B(0,2),连结AB并延长到C,连结CO,若△COB∽△CAO,则点C的坐标为( )
A.(1, )
)
B.( ,
,  )
)
C.(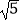 ,2
,2 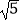 )
)
D.(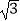 ,2
,2 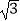 )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】数学课上,老师出了一道题:化简
[8(a+b)5-4(a+b)4+(-a-b)3]÷[2(a+b)3].
小明同学马上举手,下面是小明的解题过程:
[8(a+b)5-4(a+b)4+(-a-b)3]÷[2(a+b)3]
=[8(a+b)5-4(a+b)4+(a+b)3]÷8(a+b)3
=(a+b)2-
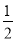 (a+b)+
(a+b)+  .
.小亮也举起了手,说小明的解题过程不对,并指了出来.老师肯定了小亮的回答.你知道小明错在哪儿吗?请指出来,并写出正确解答.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了深化课程改革,某校积极开展校本课程建设,计划成立“文学鉴赏”、“科学实验”、“音乐舞蹈”和“手工编织”等多个社团,要求每位学生都自主选择其中一个社团.为此,随机调查了本校各年级部分学生选择社团的意向,并将调查结果绘制成如下统计图表(不完整):
选择意向
所占百分比
文学鉴赏
a
科学实验
35%
音乐舞蹈
b
手工编织
10%
其他
c
根据统计图表中的信息,解答下列问题:
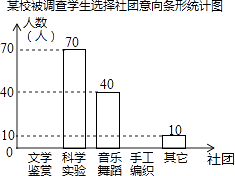
(1)本次调查的学生总人数为;
(2)补全条形统计图;
(3)将调查结果绘成扇形统计图,则“音乐舞蹈”社团所在扇形所对应的圆心角为;
(4)若该校共有1200名学生,试估计全校选择“科学实验”社团的学生人数为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,对正方形纸片ABCD进行如下操作:

(i)过点D任作一条直线与BC边相交于点E1(如图①),记∠CDE1=α1;
(ii)作∠ADE1的平分线交AB边于点E2(如图②),记∠ADE2=α2;
(iii)作∠CDE2的平分线交BC边于点E3(如图③),记∠CDE3=α3;
按此作法从操作(2)起重复以上步骤,得到α1 , α2 , …,αn , …,现有如下结论:①当α1=10°时,α2=40°;②2α4+α3=90°; ③当α5=30°时,△CDE9≌△ADE10;④当α1=45°时,BE2= .
.
其中正确的个数为( )
A.1
B.2
C.3
D.4 -
科目: 来源: 题型:
查看答案和解析>>【题目】深圳市地铁9号线梅林段的一项绿化工程由甲、乙两工程队承担,已知乙工程队单独完成这项工程所需的天数是甲工程队单独完成所需天数的
 ,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.
,甲工程队单独工作30天后,乙工程队参与合做,两队又共同工作了36天完成.
(1)求乙工程队单独完成这项工作需要多少天?
(2)因工期的需要,将此项工程分成两部分,甲做其中一部分用了x天完成,乙做另一部分用了y天完成,其中x、y均为正整数,且x<46,y<52,求甲、乙两队各做了多少天? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,O为坐标原点,平行四边形ABOC的对角线交于点M,双曲线y=
 (x<0)经过点B、M.若平行四边形ABOC的面积为12,则k= .
(x<0)经过点B、M.若平行四边形ABOC的面积为12,则k= . 
相关试题

