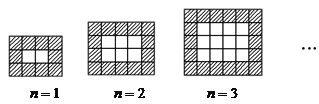
【题目】如图,用同样规格的黑白两色正方形瓷砖铺设长方形地面.请观察各图形并解答有关问题:
(1)在第![]() 个图形中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖(均用含
个图形中,每一横行共有 块瓷砖,每一竖列共有 块瓷砖(均用含![]() 的代数式表示);
的代数式表示);
(2)设铺设地面所用瓷砖的总块数为![]() ,用(1)中的
,用(1)中的![]() 表示
表示![]() ;
;
(3)当![]() =20时,求
=20时,求![]() 的值;
的值;
(4)若黑瓷砖每块4元,白瓷砖每块3元,在问题(3)中,共需花多少元购买瓷砖?
参考答案:
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)506;(4)共需花1604元购买瓷砖.
;(3)506;(4)共需花1604元购买瓷砖.
【解析】
(1)观察图形可得:n=1时,横行有(1+3)块,数列有(1+2)块,以此类推可得出规律;
(2)用每行的块数乘以每列的块数即可得到总块数;
(3)将![]() =20代入(2)中代数式求解即可;
=20代入(2)中代数式求解即可;
(4)由图形规律找到第n个图形中白瓷砖块数,总数减去白瓷砖块数等于黑瓷砖块数,再根据单价求费用即可.
解:(1)观察图形可得:n=1时,横行有(1+3)块,竖列有(1+2)块,
n=2时,横行有(2+3)块,竖列有(2+2)块,
n=3时,横行有(3+3)块,竖列有(3+2)块,
……
以此类推,第n个图中,每一横行有![]() 块,竖列有
块,竖列有![]() 块,
块,
故答案为:![]() ,
,![]() .
.
(2)![]()
(3)当![]() 时,
时,![]()
(4)由图可知:
每一横行有白瓷砖![]() 块,每一竖列有白瓷砖n块,所以白瓷砖总数是
块,每一竖列有白瓷砖n块,所以白瓷砖总数是![]() 块,
块,
当![]() =20时,黑白瓷砖共有506块,白瓷砖有
=20时,黑白瓷砖共有506块,白瓷砖有![]() 块,所以黑瓷砖有506-420=86块,
块,所以黑瓷砖有506-420=86块,
所以共需花86×4+420×3=1604元购买瓷砖.
-
科目: 来源: 题型:
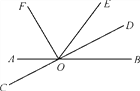
查看答案和解析>>【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2﹣4ax+3a.
(Ⅰ)求该二次函数的对称轴;
(Ⅱ)若该二次函数的图象开口向下,当1≤x≤4时,y的最大值是2,且当1≤x≤4时,函数图象的最高点为点P,最低点为点Q,求△OPQ的面积;
(Ⅲ)若对于该抛物线上的两点P(x1,y1),Q(x2,y2),当t≤x1≤t+1,x2≥5时,均满足y1≥y2,请结合图象,直接写出t的最大值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有20筐白菜,以每筐30千克为标准,超过或不足的分别用正、负来表示,记录如下:
与标准质量的差(单位:千克)
-3
-2
-1.5
0
1
2.5
筐数
1
4
2
3
2
8
(1)20筐白菜中,最重的一筐比最轻的一筐要重多少千克?
(2)与标准质量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价2元,则出售这20筐白菜可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系xoy中,点M在x轴的正半轴上,⊙M交x轴于A、B两点,交y轴于C、D两点,且C为弧AE的中点,AE交y轴于G点,若点A的坐标为(-1,0),AE=4
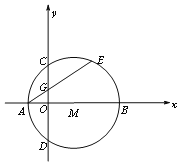
(1)求点C的坐标;
(2)连接MG、BC,求证:MG∥BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的方程2(x﹣3)﹣m=2的解和方程3x﹣7=2x的解相同.
(1)求m的值;
(2)已知线段AB=m,在直线AB上取一点P,恰好使AP=2PB,点Q为PB的中点,求线段AQ的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列图案中既是中心对称图形,又是轴对称图形的是( )
A.
 B.
B. 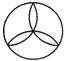 C.
C. 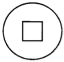 D.
D. 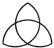
相关试题

