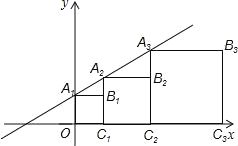
【题目】在平面直角坐标系xOy中,记直线y=x+1为l.点A1是直线l与y轴的交点,以A1O为边作正方形A1OC1B1,使点C1落在在x轴正半轴上,作射线C1B1交直线l于点A2,以A2C1为边作正方形A2C1C2B2,使点C2落在在x轴正半轴上,依次作下去,得到如图所示的图形.则点B4的坐标是 ,点Bn的坐标是 .
参考答案:
【答案】(15,8); (2n-1,2n-1).
【解析】
试题解析:把x=0代入直线y=x+1,可得:y=1,
所以可得:点B1的坐标是(1,1)
把x=1代入直线y=x+1,可得:y=2,
所以可得:点B2的坐标是(3,2),
同理可得点B3的坐标是(7,4);点B4的坐标是(15,8);
由以上得出规律是Bn的坐标为(2n-1,2n-1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只猫头鹰蹲在一棵树AC的B(点B在AC上)处,发现一只老鼠躲进短墙DF的另一侧,猫头鹰的视线被短墙遮住,为了寻找这只老鼠,它又飞至树顶C处,已知短墙高DF=4米,短墙底部D与树的底部A的距离为2.7米,猫头鹰从C点观测F点的俯角为53°,老鼠躲藏处M(点M在DE上)距D点3米.(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
(1)猫头鹰飞至C处后,能否看到这只老鼠?为什么?
(2)要捕捉到这只老鼠,猫头鹰至少要飞多少米(精确到0.1米)?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形OABC中,OA=8,OC=4,沿对角线OB折叠后,点A与点D重合, OD与BC交于点E,设点D的坐标是
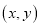 ,则
,则 的值为( )
的值为( )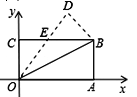
A.
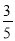 B.
B. 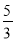 C.
C. 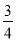 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知矩形OABC的两个顶点A、B 的坐标分别A(
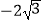 ,0)、B(
,0)、B( 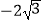 ,2),∠CAO=30°.
,2),∠CAO=30°.
(1)求对角线AC所在的直线的函数表达式;
(2)把矩形OABC以AC所在的直线为对称轴翻折,点O落在平面上的点D处,求点D的坐标;
(3)在平面内是否存在点P,使得以A、O、D、P为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果m是实数,且不等式(m+1)x>m+1的解是x<1,那么实数m的值为 __________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E、F、G、H分别为菱形ABCD四边的中点,AB=6cm,∠ABC=60°,则四边形EFGH的面积为__cm2.

-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师家距学校1900米,某天他步行去上班,走到路程的一半时发现忘带手机,此时离上班时间还有23分钟,于是他立刻步行回家取手机,随后骑电瓶车返回学校.已知李老师骑电瓶车到学校比他步行到学校少用20分钟,且骑电瓶车的平均速度是步行速度的5倍,李老师到家开门、取手机、启动电瓶车等共用4分钟.
(1)求李老师步行的平均速度;
(2)请你判断李老师能否按时上班,并说明理由.
相关试题

