【题目】如图,矩形ABCD的对角线AC,BD相交于点O,且DE∥AC,CE∥BD.
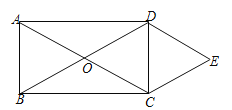
(1)求证:四边形OCED是菱形;
(2)若AB=3,AD=4,求四边形OCED的周长和面积.
参考答案:
【答案】(1)证明见解析;(2)菱形OCED的周长为![]() ,菱形OCED的面积为6.
,菱形OCED的面积为6.
【解析】
(1)首先根据两对边互相平行的四边形是平行四边形证明四边形OCED是平行四边形,再根据矩形的性质可得OC=OD,即可利用一组邻边相等的平行四边形是菱形判定出结论;
(2)先求证四边形AOED是平行四边形,从而得到OE=AD=4,然后利用菱形面积公式求其面积,利用勾股定理和矩形性质求得OD的长,从而得出该菱形的边长,则菱形周长可求.
(1)∵DE∥AC,CE∥BD
∴四边形OCED是平行四边形
∴OC=DE,OD=CE
又∵矩形ABCD的对角线AC,BD相交于点O
∴OC=OD
∴平行四边形OCED是菱形
(2)如图,连接OE,交CD于点F
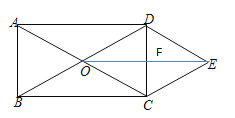
由(1)知,四边形OCED是菱形
∴OE⊥CD
又∵矩形ABCD中,AD⊥CD,CD=AB=3
∴AD∥OE
又∵DE∥AC,
∴四边形AOED是平行四边形
∴OE=AD=4
∴菱形OCED的面积:![]()
在Rt△ABD中,AB=3,AD=4
∴BD=![]() 5
5
∴![]()
∴菱形OCED的周长为![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形
 中,
中, 为
为 中点,过点
中点,过点 的直线分别与
的直线分别与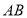 ,
,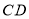 交于点
交于点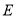 ,
,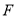 ,连结
,连结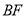 ,交
,交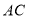 于点
于点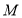 ,连结
,连结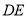 ,
,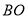 .若
.若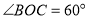 ,
,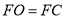 ,则下列结论:①
,则下列结论:① ;②
;②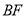 垂直平分线段
垂直平分线段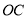 ;③
;③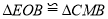 ;④四边形是
;④四边形是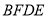 菱形.其中正确结论的个数是( )
菱形.其中正确结论的个数是( )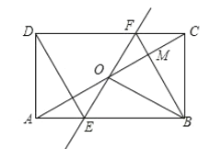
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】超速行驶是引发交通事故的主要原因.上周末,小鹏等三位同学在滨海大道红树林路段,尝试用自己所学的知识检测车速,观测点设在到公路l的距离为100米的P处.这时,一辆富康轿车由西向东匀速驶来,测得此车从A处行驶到B处所用的时间为3秒,并测得∠APO=60°,∠BPO=45°,试判断此车是否超过了每小时80千米的限制速度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一平面直角坐标系中,函数y=ax2+bx与y=bx+a的图像可能是( )
A.
 B.
B.  C.
C. 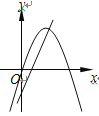 D.
D. 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是正方形,△ADF按顺时针方向旋转一定角度后得到△ABE,
若AF=4,AB=7.
(1)旋转中心为______;旋转角度为______;
(2)DE的长度为______;
(3)指出BE与DF的位置关系如何?并说明理由.
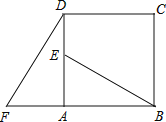
-
科目: 来源: 题型:
查看答案和解析>>【题目】去冬今春,我市部分地区遭受了罕见的旱灾,“旱灾无情人有情”.某单位给某乡中小学捐献一批饮用水和蔬菜共320件,其中饮用水比蔬菜多80件.
(1)求饮用水和蔬菜各有多少件?
(2)现计划租用甲、乙两种货车共8辆,一次性将这批饮用水和蔬菜全部运往该乡中小学.已知每辆甲种货车最多可装饮用水40件和蔬菜10件,每辆乙种货车最多可装饮用水和蔬菜各20件.则运输部门安排甲、乙两种货车时有几种方案?请你帮助设计出来;
(3)在(2)的条件下,如果甲种货车每辆需付运费400元,乙种货车每辆需付运费360元.运输部门应选择哪种方案可使运费最少?最少运费是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,CD=2,则EC的长为( )

A. 2
 B. 8 C. 2
B. 8 C. 2 D. 2
D. 2
相关试题

