【题目】如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N.下列结论:①AF⊥BG;②BN=![]() NF;③
NF;③![]() ;④
;④![]() .其中正确的结论的序号是______.
.其中正确的结论的序号是______.

参考答案:
【答案】①③.
【解析】
①易证△ABF≌△BCG,即可解题;
②易证△BNF∽△BCG,即可求得![]() 的值,即可解题;
的值,即可解题;
③作EH⊥AF,令AB=3,即可求得MN,BM的值,即可解题;
④连接AG,FG,根据③中结论即可求得S四边形CGNF和S四边形ANGD,即可解题.
①∵四边形ABCD为正方形,
∴AB=BC=CD,
∵BE=EF=FC,CG=2GD,
∴BF=CG,
∵在△ABF和△BCG中,
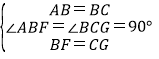 ,
,
∴△ABF≌△BCG,
∴∠BAF=∠CBG,
∵∠BAF+∠BFA=90°,
∴∠CBG+∠BFA=90°,即AF⊥BG;①正确;
②∵在△BNF和△BCG中,∠CBG=∠NBF,∠BCG=∠BNF=90°,
∴△BNF∽△BCG,
∴![]() ,
,
∴BN=![]() NF;②错误;
NF;②错误;
③作EH⊥AF,令AB=3,则BF=2,BE=EF=CF=1,

AF=![]() =
=![]() ,
,
∵S△ABF=![]() AFBN=
AFBN=![]() ABBF,
ABBF,
∴BN=![]() ,NF=
,NF=![]() BN=
BN=![]() ,
,
∴AN=AF-NF=![]() ,
,
∵E是BF中点,
∴EH是△BFN的中位线,
∴EH=![]() ,NH=
,NH=![]() ,BN∥EH,
,BN∥EH,
∴AH=![]() ,
,
![]() ,解得:MN=
,解得:MN=![]() ,
,
∴BM=BN-MN=![]() ,MG=BG-BM=
,MG=BG-BM=![]() ,
,
∴![]() ;③正确;
;③正确;
④连接AG,FG,根据③中结论,

则NG=BG-BN=![]() ,
,
∵S四边形CGNF=S△CFG+S△GNF=![]() CGCF+
CGCF+![]() NFNG=1+
NFNG=1+![]() =
=![]() ,
,
S四边形ANGD=S△ANG+S△ADG=![]() ANGN+
ANGN+![]() ADDG=
ADDG=![]() ,
,
∴S四边形CGNF≠![]() S四边形ANGD,④错误.
S四边形ANGD,④错误.
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市救灾物资储备仓库共存储了A,B,C三类救灾物资,下面的统计图是三类物资存储量的不完整统计图.
(1)求A类物资的存储量,并将两个统计表补充完整;
(2)现计划租用甲、乙两种货车共8辆,一次性将A、B两类物资全部运往某灾区.已知甲种货车最多可装A类物资10吨和B类物资40吨,乙种货车最多可装A、B类物资各20吨,则物资储备仓库安排甲、乙两种货车有几种方案?请你帮助设计出来.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某养殖户每年的养殖成本包括固定成本和可变成本,其中固定成本每年均为4万元,可变成本逐年增长,已知该养殖户第一年的可变成本为2.6万元,设可变成本平均每年增长的百分率为

(1)用含x的代数式表示低3年的可变成本为 万元;
(2)如果该养殖户第3年的养殖成本为7.146万元,求可变成本平均每年的增长百分率x.
-
科目: 来源: 题型:
查看答案和解析>>【题目】李老师为了了解学生暑期在家的阅读情况,随机调查了20名学生某一天的阅读小时数,具体情况统计如下:
阅读时间
(小时)
2
2.5
3
3.5
4
学生人数(名)
1
2
8
6
3
则关于这20名学生阅读小时数的说法正确的是( )
A. 众数是8 B. 中位数是3 C. 平均数是3 D. 方差是0.34
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系xOy中,点A、B的横坐标分别为a、
 ,二次函数
,二次函数 的图象经过点A、B,且a、m满足
的图象经过点A、B,且a、m满足 为常数
为常数 .
. 若一次函数
若一次函数 的图象经过A、B两点.
的图象经过A、B两点. 当
当 、
、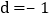 时,求k的值;
时,求k的值; 若y随x的增大而减小,求d的取值范围;
若y随x的增大而减小,求d的取值范围; 当
当 且
且 、
、 时,判断直线AB与x轴的位置关系,并说明理由;
时,判断直线AB与x轴的位置关系,并说明理由; 点A、B的位置随着a的变化而变化,设点A、B运动的路线与y轴分别相交于点C、D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.
点A、B的位置随着a的变化而变化,设点A、B运动的路线与y轴分别相交于点C、D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠长方形纸片ABCD的一边AD,使点D落在BC边上的点F处,已知AB=8cm,BC=10cm,则折痕AE的长为( )

A.
 cmB.
cmB. cmC.12cmD.13 cm
cmC.12cmD.13 cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求PQ的长.
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.

相关试题

