【题目】如图,已知△ABC中,∠B=90°,AB=16cm,BC=12cm,P、Q是△ABC边上的两个动点,其中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C→A方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒.
(1)出发2秒后,求PQ的长.
(2)当点Q在边BC上运动时,出发几秒钟后,△PQB能形成等腰三角形?
(3)当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形
;(3)当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形
【解析】
(1)根据点P、Q的运动速度求出AP,再求出BP和BQ,用勾股定理求得PQ即可;
(2)设出发t秒钟后,△PQB能形成等腰三角形,则BP=BQ,由BQ=2t,BP=8-t,列式求得t即可;
(3)当点Q在边CA上运动时,能使△BCQ成为等腰三角形的运动时间有三种情况:
①当CQ=BQ时,则∠C=∠CBQ,可证明∠A=∠ABQ,则BQ=AQ,则CQ=AQ,从而求得t;
②当CQ=BC时,则BC+CQ=12,易求得t;
③当BC=BQ时,过B点作BE⊥AC于点E,则求出BE,CE,即可得出t.
(1)∵BQ=2×2=4(cm),BP=ABAP=162×1=14(cm ),∠B=90°,
∴PQ=![]() =
=![]() (cm);
(cm);
(2)BQ=2t,BP=16t,
根据题意得:2t=16t,
解得:t=![]() ,
,
即出发![]() 秒钟后,△PQB能形成等腰三角形;
秒钟后,△PQB能形成等腰三角形;
(3)①当CQ=BQ时,如图1所示,
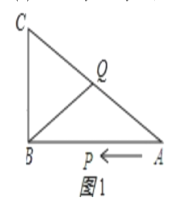
则∠C=∠CBQ,
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°.
∠A+∠C=90°,
∴∠A=∠ABQ,
∴BQ=AQ,
∴CQ=AQ=10,
∴BC+CQ=22,
∴t=22÷2=11秒。
②当CQ=BC时,如图2所示,

则BC+CQ=24,
∴t=24÷2=12秒。
③当BC=BQ时,如图3所示,
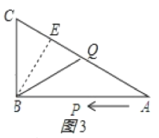
过B点作BE⊥AC于点E,
则BE=![]() ,
,
∴CE=![]() ,
,
∴CQ=2CE=14.4,
∴BC+CQ=26.4,
∴t=26.4÷2=13.2秒。
综上所述:当t为11秒或12秒或13.2秒时,△BCQ为等腰三角形
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工厂有甲、乙两台机器加工同一种零件,已知一小时甲加工的零件数与一小时乙加工的零件数的和为36个,甲加工80个零件与乙加工100个零件的所用时间相等.求甲、乙两台机器每小时分别加工零件多少个?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰三角形ABC中,AB=AC.
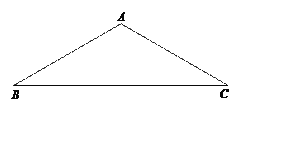
(1)用尺规作出圆心在直线BC上,且过A、C两点的⊙O;(注:保留作图痕迹,标出点O,并写出作法)
(2)若∠B=30°,求证:AB与(1)中所作⊙O相切.
-
科目: 来源: 题型:
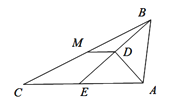
查看答案和解析>>【题目】如图,在△ABC中,点E是边AC上一点,线段BE垂直于∠BAC的平分线于点D,点M为边BC的中点,连接DM.
(1)求证: DM=
 CE;
CE; (2)若AD=6,BD=8,DM=2,求AC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察算式:1×3+1=4=22;2×4+1=9=32;3×5+1=16=42;4×6+1=25=52,…
(1)请根据你发现的规律填空:6×8+1=( )2;
(2)用含n的等式表示上面的规律: ;
(3)用找到的规律解决下面的问题:
计算:(1+
 )(1+
)(1+ )(1+
)(1+ )(1+
)(1+ )…(1+
)…(1+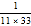 )
) -
科目: 来源: 题型:
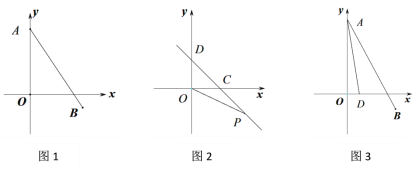
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知A(0,5), B(a,b),且a,b满足b=
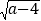 +
+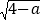 -1.
-1.(1)如图,求线段AB的长;
(2)如图,直线CD与x轴、y轴正半轴分别交于点C,D,∠OCD=45°,第四象限的点P(m,n)在直线CD上,且mn=-6,求OP2-OC2的值;
(3)如图,若点D(1,0),求∠DAO +∠BAO的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队都参与某筑路工程,先由甲队筑路60千米,再由乙队完成剩下的筑路工程,已知乙队筑路总千米数是甲队筑路总千米数的
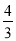 倍,甲队比乙队多筑路20天.如果甲、乙两队平均每天筑路千米数之比为5∶8,求乙队平均每天筑路多少千米?
倍,甲队比乙队多筑路20天.如果甲、乙两队平均每天筑路千米数之比为5∶8,求乙队平均每天筑路多少千米?
相关试题

