【题目】将正方形 ABCD (如图 1)作如下划分:
第1次划分:分别连接正方形ABCD对边的中点(如图2),得线段HF和EG,它们交于点M,此时图2中共有5个正方形;
第2次划分:将图2 左上角正方形AEMH再作划分,得图3,则图3 中共有9个正方形;
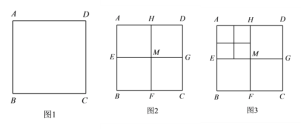
(1)若每次都把左上角的正方形依次划分下去,则第100次划分后,图中共有 个正方形;
(2)继续划分下去,第几次划分后能有805个正方形?写出计算过程.
(3)按这种方法能否将正方形ABCD划分成有2015个正方形的图形?如果能,请算出是第几次划分,如果不能,需说明理由.
(4)如果设原正方形的边长为1,通过不断地分割该面积为1的正方形,并把数量关系和几何图形巧妙地结合起来,可以很容易得到一些计算结果,试着探究求出下面表达式的结果吧.
计算 ![]() .( 直接写出答案即可)
.( 直接写出答案即可)
参考答案:
【答案】(1)401;(2)第 201 次划分后能有 805个正方形;(3)不能;(4)![]()
【解析】
(1)由第一次可得5个正方形,第二次可得9个正方形,第三次可得13个正方形,可得规律:第n次可得(4n+1)个正方形,继而求得答案;
(2)由规律可得方程4n+1=805,继而求得答案;
(3)由规律可得4n+1=2015,又由n为整数,可求得答案;
(4)此题可看作上面几何体面积问题,即可求得答案.
(1)∵第一次可得5个正方形,第二次可得9个正方形,第三次可得13个正方形,
∴第n次可得(4n+1)个正方形,
∴第100次可得正方形:4×100+1=401(个);
故答案为:401;
(2)根据题意得:4n+1=805,
解得:n=201;
∴第201次划分后能有805个正方形;
(3)不能,
∵4n+1=2015,
解得:n=503.5,
∴n不是整数,
∴不能将正方形性ABCD划分成有2015个正方形的图形;
(4)结合题意得:
![]()
=![]()
=![]()
=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】蜗牛从某点
 开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米): ,
, ,
, ,
, ,
, ,
, ,
, .
. 通过计算说明蜗牛是否回到起点
通过计算说明蜗牛是否回到起点 .
. 蜗牛离开出发点
蜗牛离开出发点 最远时是多少厘米?
最远时是多少厘米? 在爬行过程中,如果每爬
在爬行过程中,如果每爬 厘米奖励
厘米奖励 粒芝麻,则蜗牛一共得到多少粒芝麻?
粒芝麻,则蜗牛一共得到多少粒芝麻? -
科目: 来源: 题型:
查看答案和解析>>【题目】近年来,手机微信红包迅速流行起来.去年春节,小米的爷爷也尝试用微信发红包,他分别将10元、30元、60元的三个红包发到只有爷爷、爸爸、妈妈和小米的微信群里,他们每人只能抢一个红包,且抢到任何一个红包的机会均等(爷爷只发不抢,红包里钱的多少与抢红包的先后顺序无关).
(1)求小米抢到60元红包的概率;
(2)如果小米的奶奶也加入“抢红包”的微信群,他们四个人中将有一个人抢不到红包,那么这种情况下,求小米和妈妈两个人抢到红包的钱数之和不少于70元的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,梯形ABCD中,AB∥CD,BC⊥AB,AB=AD,连接BD(如图a),点P沿梯形的边,从点A→B→C→D→A移动,设点P移动的距离为x,BP=y.
(1)求证:∠A=2∠CBD;
(2)当点P从点A移动到点C时,y与x的函数关系如图(b)中的折线MNQ所示,试求CD的长.
(3)在(2)的情况下,点P从A→B→C→D→A移动的过程中,△BDP是否可能为等腰三角形?若能,请求出所有能使△BDP为等腰三角形的x的取值;若不能,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,正比例函数y=x的图象与一次函数y=kx﹣k的图象的交点坐标为A(m,2).
(1)求m的值和一次函数的解析式;
(2)设一次函数y=kx﹣k的图象与y轴交于点B,求△AOB的面积;
(3)直接写出使函数y=kx﹣k的值大于函数y=x的值的自变量x的取值范围.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.
(1)求证:△AEC≌△ADB;
(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】图1为全体奇数排成的数表,用十字框任意框出5个数,记框内中间这个数为 a(如图2).
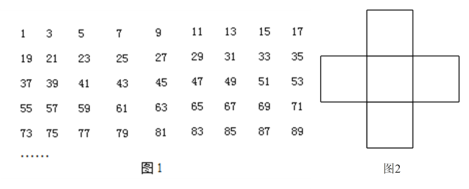
(1)请用含a的代数式表示框内的其余4个数;
(2)框内的5个数之和能等于 2015,2020 吗?若不能,请说明理由;若能,请求出这5个数中最小的一个数,并写出最小的这个数在图1数表中的位置.(自上往下第几行,自左往右的第几个)
相关试题

