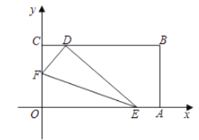
【题目】如图,将一矩形纸片![]() 放在平面直角坐标系中,
放在平面直角坐标系中,![]() ,
,![]() ,
,![]() .动点
.动点![]() 从点
从点![]() 出发以每秒1个单位长度的速度沿
出发以每秒1个单位长度的速度沿![]() 向终点
向终点![]() 运动,运动
运动,运动![]() 秒时,动点
秒时,动点![]() 从点
从点![]() 出发以相同的速度沿
出发以相同的速度沿![]() 向终点
向终点![]() 运动,当点
运动,当点![]() 、
、![]() 其中一点到达终点时,另一点也停止运动.设点
其中一点到达终点时,另一点也停止运动.设点![]() 的运动时间为
的运动时间为![]() (秒).
(秒).

(Ⅰ)![]() _____________,
_____________,![]() _____________;(用含
_____________;(用含![]() 的代数式表示)
的代数式表示)
(Ⅱ)当![]() 时,将
时,将![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处.
处.
①求点![]() 的坐标及直线
的坐标及直线![]() 的解析式;
的解析式;
②点![]() 是射线
是射线![]() 上的任意一点,过点
上的任意一点,过点![]() 作直线
作直线![]() 的平行线,与
的平行线,与![]() 轴交于
轴交于![]() 点,设直线
点,设直线![]() 的解析式为
的解析式为![]() ,当点
,当点![]() 与点
与点![]() 不重合时,
不重合时,![]() 为
为![]() 的面积,当点
的面积,当点![]() 与点
与点![]() 重合时,
重合时,![]() .求
.求![]() 与
与![]() 之间的函数关系式,并求出自变量
之间的函数关系式,并求出自变量![]() 的取值范围.
的取值范围.
参考答案:
【答案】(Ⅰ)![]() ;
;![]() ;(Ⅱ)①
;(Ⅱ)①![]() ;②
;②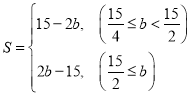
【解析】
(I)由O(0,0),A(6,0),C(0,3),可得:OA=6,OC=3,根据矩形的对边平行且相等,可得:AB=OC=3,BC=OA=6,进而可得点B的坐标为:(6,3),然后根据E点与F点的运动速度与运动时间即可用含t的代数式表示OE,OF;
(II)①由翻折的性质可知:△OPF≌△DPF,进而可得:DF=OF,然后由t=1时,DF=OF=![]() ,CF=OC-OF=
,CF=OC-OF=![]() ,然后利用勾股定理可求CD的值,进而可求点D和E的坐标;利用待定系数可得直线DE的解析式;
,然后利用勾股定理可求CD的值,进而可求点D和E的坐标;利用待定系数可得直线DE的解析式;
②先确定出k的值,再分情况计算S的表达式,并确认b的取值.
解:(I)∵O(0,0),A(6,0),C(0,3),
∴OA=6,OC=3,
∵四边形OABC是矩形,
∴AB=OC=3,BC=OA=6,
∴B(6,3),
∵动点F从O点以每秒1个单位长的速度沿OC向终点C运动,运动![]() 秒时,动点E从点A出发以相等的速度沿AO向终点O运动.
秒时,动点E从点A出发以相等的速度沿AO向终点O运动.
∴当点E的运动时间为t(秒)时,
∴AE=t,OF=![]() +t,
+t,
则OE=OA-AE=6-t;
故答案为:![]() ;
;![]() .
.
(Ⅱ)①当![]() 时,
时,![]() .
.
∵![]() , ∴
, ∴![]() .
.
∴![]() .
.
∵![]() 沿
沿![]() 翻折得到
翻折得到![]() ,
,
∴![]() .
.
在![]() 中,利用勾股定理,得
中,利用勾股定理,得![]() .
.
∵四边形![]() 是矩形,
是矩形,
∴![]() .
.
设直线![]() 的解析式为:
的解析式为:![]() .
.
∵将![]() ,
,![]() 代入
代入![]()
![]() ,解得
,解得 .
.
∴直线![]() 的解析式为:
的解析式为:![]() .
.
②∵直线![]() 与直线
与直线![]() 平行,
平行,
∴![]() .
.
∴该直线解析式为:![]() .
.
令![]() 时,
时,![]() ,∴
,∴![]()
如图所示:当点![]() 在线段
在线段![]() 上时,
上时,
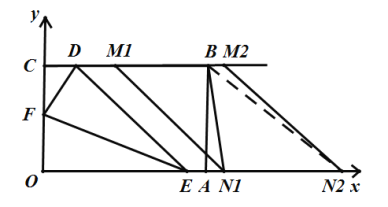
∴![]() .
.
![]() ,(
,(![]() ).
).
当点![]() 与点
与点![]() 重合时,
重合时,![]() ,
,![]() .
.
当在![]() 的延长线上时,
的延长线上时,
∴![]() .
.
![]() ,(
,(![]() ).
).
综上所述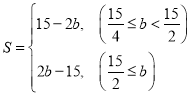
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,对角线AC、BD相交于点O,且OA=OB
(1)求证:四边形ABCD是矩形;
(2)若AB=5,∠AOB=60°,求BC的长.

-
科目: 来源: 题型:
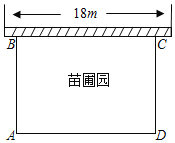
查看答案和解析>>【题目】某中学课外兴趣活动小组准备围建一个矩形的苗圃圆.其中一边靠墙,另外三边用长为40m的篱笆围成.已知墙长为18m(如图所示),设这个苗圃园垂直于墙的一边AB为xm
(1)用含有x的式子表示AD,并写出x的取值范围;
(2)若苗圃园的面积为192m2平方米,求AB的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有4个分别标有数字-1,-2,3,4的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y.
(1)小红摸出标有数字3的小球的概率是________;
(2)请用列表或画树状图的方法表示出由x,y确定的点P(x,y)所有可能的结果;
(3)若规定:点P(x,y)在第一象限或第三象限小红获胜,点P(x,y)在第二象限或第四象限小颖获胜,请分别求出两人获胜的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】课外阅读是提高学生素养的重要途径.某校为了解本校学生课外阅读情况,对九年级学生进行随机抽样调查.如图是根据调查结果绘制成的统计图(不完整),请根据图中提供的信息,解答下面的问题:
(1)本次抽样调查的样本容量是____ ____;
(2)在条形统计图补中,计算出日人均阅读时间在0.5~1小时的人数是____ ____,并将条形统计图补充完整;
(3)在扇形统计图中,计算出日人均阅读时间在1~1.5小时对应的圆心角度数____ ____度;
(4)根据本次抽样调查,试估计该市15000名九年级学生中日人均阅读时间在0.5~1.5小时的人数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
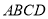 的边长为
的边长为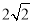 ,点
,点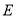 、
、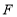 在
在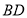 上,且
上,且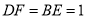 ,四边形
,四边形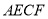 的面积为__________.
的面积为__________.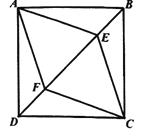
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个3×3的方格中填写了9个数字,使得每行、每列、每条对角线上的三个数之和相等,得到的3×3的方格称为一个三阶幻方.
(1)在图1中空格处填上合适的数字,使它构成一个三阶幻方;
(2)如图2的方格中填写了一些数和字母,当x+y的值为多少时,它能构成一个三阶幻方.

相关试题

