【题目】如图,在△ABC中,已知AB=AC,D、E、B、C在同一条直线上,且AB2=BDCE,求证:△ABD∽△ECA.
参考答案:
【答案】证明:
∵AB=AC,
∴∠ABC=∠ACB,
∴∠ABD=∠ACE,
∵AB2=BDCE,
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() ,
,
∴△ABD∽△ECA
【解析】由条件可得到∠ABD=∠ACE,结合AB2=BDCE和AB=AC,可得到 ![]() =
= ![]() ,即可证得结论.
,即可证得结论.
【考点精析】掌握相似三角形的判定是解答本题的根本,需要知道相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,∠B的角平分线BE与AD交于点E,∠BED的角平分线EF与DC交于点F,若AB=9,DF=2FC,则BC= . (结果保留根号)

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图1,
 ,求
,求 的度数. (提示:作
的度数. (提示:作 ).
). (2)如图2,
 ,当点
,当点 在线段
在线段 上运动时,
上运动时, ,求
,求 与
与 、
、 之间的数量关系,并说明理由.
之间的数量关系,并说明理由. (3)在(2)的条件下,如果点
 在射线
在射线 上运动,请你直接写出
上运动,请你直接写出 与
与 、
、 之间的数量关系.
之间的数量关系.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,矩形ABCO的边OC、OA,分别在x轴、y轴上,点E在边BC上,将该矩形沿AE折叠,点B恰好落在边OC上的F处,若OA=8,CF=4,则点E的坐标是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)(
 )×(-6)+(-
)×(-6)+(-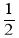 )2÷(-
)2÷(-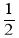 )3
)3(2)-12018-(1-0.5)×
 ×[2-(-3)3]
×[2-(-3)3](3)(-1
 +2
+2 -1
-1 )÷(-
)÷(- ).
). -
科目: 来源: 题型:
查看答案和解析>>【题目】一个由若干小正方形堆成的几何体,它从正面看和从左面看的图形如图1所示.
 这个几何体可以是图2中甲,乙,丙中的______;
这个几何体可以是图2中甲,乙,丙中的______; 这个几何体最多由______个小正方体堆成,最少由______个小正方体堆成;
这个几何体最多由______个小正方体堆成,最少由______个小正方体堆成; 请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形.
请在图3中用阴影部分画出符合最少情况时的一个从上面往下看得到的图形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,
 =
=  =
=  ,那么△ABD与△BCE相似吗?为什么?
,那么△ABD与△BCE相似吗?为什么? 
相关试题

