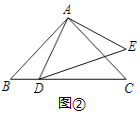
【题目】基本图形:在RT△ABC中,AB=AC,D为BC边上一点(不与点B,C重合),将线段AD绕点A逆时针旋转90°得到AE.
探索:(1)连接EC,如图①,试探索线段BC,CD,CE之间满足的等量关系,并证明结论;
(2)连接DE,如图②,试探索线段DE,BD,CD之间满足的等量关系,并证明结论;
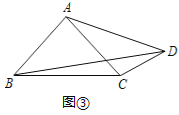
联想:(3)如图③,在四边形ABCD中,∠ABC=∠ACB=∠ADC=45°,若BD=7,CD=2,则AD的长为 .

参考答案:
【答案】(1)结论:![]() .证明见解析;(2)结论:
.证明见解析;(2)结论:![]() .证明见解析;(3)
.证明见解析;(3)![]()
【解析】
(1)说明△BAD≌OCAE(SAS)即可解答;
(2)先说明△BAD≌△CAE,可得BD=CE、∠ACE=∠B,进一步可得∠DCE=90°,最后利用勾股定理即可解答;
(3)作AE⊥AD.使AE=AD,连接CE,DE.由△BAD≌△CAE(SAS),推出BD=CE=7,由∠ADC=45°,∠EDA=45°,可得∠EDC=90°,最后利用勾股定理解答即可
解:(1)结论:![]() ,理由如下:
,理由如下:
如图①中,

∵![]() ,
,
∴![]() ,即
,即![]() ,
,
在![]() 和
和![]() 中,
中,
 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即:![]() ;
;
(2)结论:![]() .理由如下:连接CE,
.理由如下:连接CE,

由(1)得,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∴![]()
(3)作AE⊥4D,使4E=AD,连接CE,DE.
∴∠BAC+∠CAD=∠DAE+∠CAD,即∠BAD=∠CAE,
在△BAD与△CAE中,
AB=AC,∠BAD=∠CAE,AD=AE
∴△BAD≌△CAE(SAS),
∴BD=CE=7,
∵∠ADC=45°,∠EDA=45°,
∴∠EDC=90°。
∴DE=![]() =√8.
=√8.
∵∠DAE=90°
∴![]() ,即
,即![]()
∴AD=![]() .
.
故答案为![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC中,AB=BC,DE⊥AB于点E,DF⊥BC于点D,交AC于F.
⑴若∠AFD=155°,求∠EDF的度数;
⑵若点F是AC的中点,求证:∠CFD=
 ∠B.
∠B.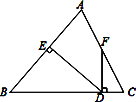
-
科目: 来源: 题型:
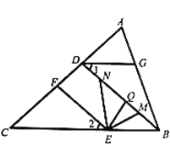
查看答案和解析>>【题目】如图,已知
 ,
,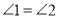 ,点
,点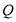 是线段
是线段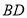 上一点(不与端点
上一点(不与端点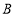 重合),
重合),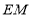 、
、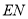 分别平分
分别平分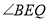 和
和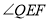 交
交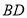 于点
于点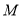 、
、 .
.
(1)请说明:
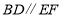 ;
;(2)当点
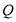 在
在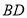 上移动时,请写出
上移动时,请写出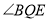 和
和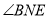 之间满足的数量关系为______;
之间满足的数量关系为______;(3)若
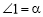 ,则当点
,则当点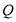 移动到使得
移动到使得 时,请直接写出
时,请直接写出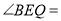 ______(用含
______(用含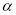 的代数式表示).
的代数式表示). -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两个工程队计划修建一条长15千米的乡村公路,已知甲工程队每天比乙工程队每天多修路0.5千米,乙工程队单独完成修路任务所需天数是甲工程队单独完成修路任务所需天数的1.5倍.
(1)求甲、乙两个工程队每天各修路多少千米?
(2)若甲工程队每天的修路费用为0.5万元,乙工程队每天的修路费用为0.4万元,要使两个工程队修路总费用不超过5.2万元,甲工程队至少修路多少天?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为调查广西北部湾四市市民上班时最常用的交通工具的情况,随机抽取了四市部分市民进行调查,要求被调查者从“A:自行车,B:电动车,C:公交车,D:家庭汽车,E:其他”五个选项中选择最常用的一项,将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题:

(1)在这次调查中,一共调查了 名市民,扇形统计图中,C组对应的扇形圆心角是 °;
(2)请补全条形统计图;
(3)若甲、乙两人上班时从A、B、C、D四种交通工具中随机选择一种,则甲、乙两人恰好选择同一种交通工具上班的概率是多少?请用画树状图或列表法求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB,AC边上的中点,连接DE,将△ADE绕点E旋转180°得到△CFE,连接AF,AC.

(1)求证:四边形ADCF是菱形;
(2)若BC=8,AC=6,求四边形ABCF的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】松雷中学图书馆近日购进甲、乙两种图书,每本甲图书的进价比每本乙图书的进价高20元,花780元购进甲图书的数量与花540元购进乙图书的数量相同.
(1)求甲、乙两种图书每本的进价分别是多少元?
(2)松雷中学计划购进甲、乙两种图书共70本,总购书费用不超过4000元,则最多购进甲种图书多少本?
相关试题

