【题目】如图,我渔政310船在南海海面上沿正东方向匀速航行,在A地观测到我渔船C在东北方向上的我国某传统渔场.若渔政310船航向不变,航行半小时后到达B处,此时观测到我渔船C在北偏东30°方向上.问渔政310船再航行多久,离我渔船C的距离最近?(假设我渔船C捕鱼时移动距离忽略不计,结果不取近似值.)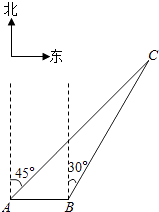
参考答案:
【答案】解:作CD⊥AB交AB的延长线于点D.
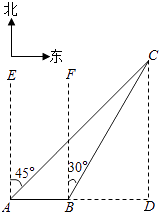
∵A地观测到渔船C在东北方向上,渔船C在北偏东30°方向上,
∴∠CAB=45°,∠CBD=60°.
在Rt△BCD中,∵∠CDB=90°,∠CBD=60°,
∴CD= ![]() BD.
BD.
在Rt△ACD中,∵∠CDA=90°,∠CAD=45°,
∴CD=AD,
∴ ![]() BD=AB+BD,
BD=AB+BD,
∴ ![]() =
= ![]() =
= ![]() ,
,
设渔政310船再航行t分钟,离我渔船C的距离最近,
则 ![]() =
= ![]() ,
,
解得t=15 ![]() +15.
+15.
答:渔政310船再航行(15 ![]() +15)分钟,离我渔船C的距离最近.
+15)分钟,离我渔船C的距离最近.
【解析】作CD⊥AB交AB的延长线于点D.易得到∠CAB=45°,∠CBD=60°,在Rt△BCD中求出CD=![]() BD,在Rt△ACD中,求得
BD,在Rt△ACD中,求得![]() 的值,然后根据匀速行驶的渔船其时间之比等于路程之比,从而求出渔船行驶BD的路程所需的时间。
的值,然后根据匀速行驶的渔船其时间之比等于路程之比,从而求出渔船行驶BD的路程所需的时间。
【考点精析】本题主要考查了解直角三角形和关于方向角问题的相关知识点,需要掌握解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法);指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.

(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一批男衬衫,经过抽样调查60名中年男子,得知所需衬衫型号的人数如表所示.求出它的中位数是74,众数是76,平均数是74.6,下列说法正确的是( )

A. 所需78号人数太少,78号的可以不生产
B. 这批衬衫可以一律按身长是74.6这个平均数生产
C. 因为众数是76,故76号的生产量要占第一位
D. 因为中位数是74,故74号的生产量要占第一位
-
科目: 来源: 题型:
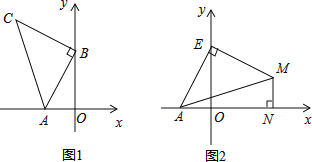
查看答案和解析>>【题目】如图1,
 ,
, ,以B点为直角顶点在第二象限作等腰直角
,以B点为直角顶点在第二象限作等腰直角 .
.
 求C点的坐标;
求C点的坐标; 在坐标平面内是否存在一点P,使
在坐标平面内是否存在一点P,使 与
与 全等?若存在,直接写出P点坐标,若不存在,请说明理由;
全等?若存在,直接写出P点坐标,若不存在,请说明理由; 如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角
如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角 ,过M作
,过M作 轴于N,直接写出
轴于N,直接写出 的值为 .
的值为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】有100名学生参加两次科技知识测试,条形图显示两次测试的分数分布情况如图所示:根据条形图提供的信息,下列说法中,正确的是( )
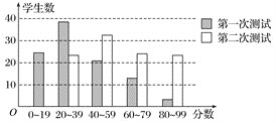
A. 两次测试,最低分在第二次测试中
B. 第一次测试和第二次测试的平均分相同
C. 第一次分数的中位数在20~39分数段
D. 第二次分数的中位数在60~79分数段
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,要设计一个等腰梯形的花坛,花坛上底120米,下底180米,上下底相距80米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为x米.

(1)用含x的式子表示横向甬道的面积;
(2)当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
(3)根据设计的要求,甬道的宽不能超过6米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是5.7,花坛其余部分的绿化费用为每平方米0.02万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元? -
科目: 来源: 题型:
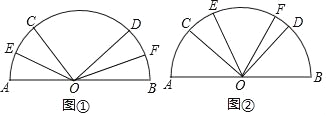
查看答案和解析>>【题目】点C,D是半圆弧上的两个动点,在运动的过程中保持∠COD=100°.
(1)如图①,OE平分∠AOC,OF平分∠BOD,求∠EOF的度数;
(2)如图②,已知∠AOC的度数为x,OE平分∠AOD,OF平分∠BOC,求∠EOF的度数.
相关试题

