【题目】为了提高服务质量,某宾馆决定对甲、乙两种套房进行星级提升,已知甲种套房提升费用比乙种套房提升费用少3万元,如果提升相同数量的套房,甲种套房费用为625万元,乙种套房费用为700万元.
(1)甲、乙两种套房每套提升费用各多少万元?
(2)如果需要甲、乙两种套房共80套,市政府筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于甲、乙种套房星级提升,市政府对两种套房的提升有几种方案?哪一种方案的提升费用最少?
(3)在(2)的条件下,根据市场调查,每套乙种套房的提升费用不会改变,每套甲种套房提升费用将会提高a万元(a>0),市政府如何确定方案才能使费用最少?
参考答案:
【答案】
(1)解:设甲种套房每套提升费用为x万元,依题意,
得 ![]() 解得:x=25
解得:x=25
经检验:x=25符合题意,x+3=28
答:甲,乙两种套房每套提升费用分别为25万元,28万元
(2)解:设甲种套房提升m套,那么乙种套房提升(80﹣m)套,依题意,得
![]()
解得:48≤m≤50
即m=48或49或50,所以有三种方案分别是:
方案一:甲种套房提升48套,乙种套房提升32套.
方案二:甲种套房提升49套,乙种套房提升31套,
方案三:甲种套房提升50套,乙种套房提升30套.
设提升两种套房所需要的费用为W万元.则
W=25m+28×(80﹣m)=﹣3m+2240,
∵k=﹣3<0,
∴W随m的增大而减小,
∴当m=50时,W最少=2090万元,即第三种方案费用最少
(3)解:在(2)的基础上有:W=(25+a)m+28×(80﹣m)=(a﹣3)m+2240
当a=3时,三种方案的费用一样,都是2240万元.
当a>3时,k=a﹣3>0,
∴W随m的增大而增大,
∴m的值越小时,费用W最小.
当0<a<3时,k=a﹣3<0,
∴W随m的增大而减小,
∴m的值越大时,W最小,费用最省
【解析】(1)设甲种套房每套提升费用为x万元,根据题意建立方程求出其解即可;(2)设甲种套房提升m套,那么乙种套房提升(80﹣m)套,根据条件建立不等式组求出其解就可以求出提升方案,再表示出总费用与m之间的函数关系式,根据一次函数的性质就可以求出结论;(3)根据(2)表示出W与m之间的关系式,由一次函数的性质分类讨论就可以得出结论.
【考点精析】本题主要考查了分式方程的应用和一元一次不等式组的应用的相关知识点,需要掌握列分式方程解应用题的步骤:审题、设未知数、找相等关系列方程、解方程并验根、写出答案(要有单位);1、审:分析题意,找出不等关系;2、设:设未知数;3、列:列出不等式组;4、解:解不等式组;5、检验:从不等式组的解集中找出符合题意的答案;6、答:写出问题答案才能正确解答此题.
-
科目: 来源: 题型:
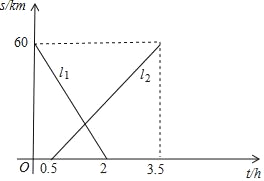
查看答案和解析>>【题目】A,B两地相距60km,甲、乙两人从两地出发相向而行,甲先出发.图中
 表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:
表示两人离A地的距离s(km)与时间t(h)的关系,请结合图象解答下列问题:(1)表示乙离A地的距离与时间关系的图象是 (填
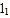 或
或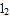 );
);(2)甲的速度是 km/h,乙的速度是 km/h;
(3)甲出发多少小时两人恰好相距5km?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,B,C两点把线段AD分成2:5:3三部分,M为AD的中点,BM=6cm,求CM和AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】今年以来,我国持续大面积的雾霾天气让环保和健康问题成为焦点.为了调查学生对雾霾天气知识的了解程度,某校在学生中做了一次抽样调查,调查结果共分为四个等级:A.非常了解;B.比较了解;C.基本了解;D.不了解.根据调查统计结果,绘制了不完整的三种统计图表. 对雾霾了解程度的统计表:
对雾霾的了解程度
百分比
A.非常了解
5%
B.比较了解
m
C.基本了解
45%
D.不了解
n
请结合统计图表,回答下列问题.
对雾霾天气了解程度的条形统计图
对雾霾天气了解程度的扇形统计图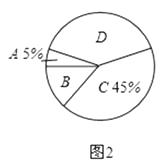
(1)本次参与调查的学生共有人,m= , n=;
(2)图2所示的扇形统计图中D部分扇形所对应的圆心角是度;
(3)请补全图1示数的条形统计图;
(4)根据调查结果,学校准备开展关于雾霾知识竞赛,某班要从“非常了解”态度的小明和小刚中选一人参加,现设计了如下游戏来确定,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4,然后放到一个不透明的袋中,一个人先从袋中随机摸出一个球,另一人再从剩下的三个球中随机摸出一个球.若摸出的两个球上的数字和为奇数,则小明去;否则小刚去.请用树状图或列表法说明这个游戏规则是否公平. -
科目: 来源: 题型:
查看答案和解析>>【题目】列方程解应用题:
为了缓解北京市西部地区的交通拥堵现象,市政府决定修建本市的第一条磁浮地铁线路﹣﹣“S1线”.该线路连接北京城区与门头沟,西起石门营,向东经苹果园,终点至慈寿寺与6号线和10号线相接.为使该工程提前4个月完成,在保证质量的前提下,必须把工作效率提高10%.问原计划完成这项工程需用多少个月.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程mx2﹣3(m+1)x+2m+3=0
(1)如果该方程有两个不相等的实数根,求m的取值范围;
(2)在(1)的条件下,当该方程的根都是整数,且|x|<4时,求m的整数值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】商场打折前,买1件A商品和1件B商品用了20元,买30件A商品和40件B商品用了680元.打折后,买100件A商品100件B商品用了1800元.请根据上述信息解决下列问题:
(1)打折前A、B两种商品的单价分别是多少?
(2)请在(1)的基础上提出一个能使题目剩余条件解决的问题,并加以解决.
相关试题

