搜索
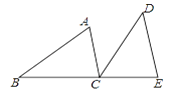
【题目】如图，B、C、E三点在同一条直线上，AC∥DE，AC=CE，BC=DE．
（1）求证：∠ACD=∠B；
（2）若∠A=40°，求∠BCD的度数．
参考答案：
【答案】（1）证明见解析；（2）140°．
【解析】试题分析：（1）根据平行线的性质可得∠ACB=∠DEC，∠ACD=∠D，再由∠ACD=∠B可得∠D=∠B，然后可利用AAS证明△ABC≌△CDE，进而得到CB=DE；
（2）根据全等三角形的性质可得∠A=∠DCE=40°，然后根据邻补角的性质进行计算即可．
试题解析：（1）证明：∵AC∥DE， ∴∠ACB=∠E，∠ACD=∠D，在△ACB和△CDB中，
，∴△ABC≌△CDE，∴∠B=∠D，∴∠ACD=∠B
（2）解：∵△ABC≌△CDE， ∴∠A=∠DCE=40°，∴∠BCD=180°﹣∠ECD=140°．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知直线y=mx+n（m，n为常数）经过点（0，﹣2）和（3，0），则关于x的方程mx+n=0的解为（ ）
A. x=0 B. x=1 C. x=﹣2 D. x=3
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，下面四个结论正确的有________________．
①BP=CM；②△ABQ≌△CAP；③∠CMQ的度数不变，始终等于60°；④当第
秒或第
秒时，△PBQ为直角三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）尺规作图：如图1，在四边形ABCD内找一点P，使得点P到AB、BC的距离相等，并且点P到点A、D的距离也相等．（不写作法，保留作图痕迹）．
（2）如图2，在长度为1个单位长度的小正方形组成的正方形网格中，点A、B、C在小正方形的顶点上，①△ABC的面积为______．
②在图中画出与△ABC关于直线l成轴对称的△A1B1C1．
-
科目： 来源： 题型：
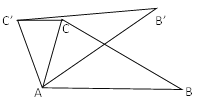
查看答案和解析>>【题目】如图，在△ABC中，∠CAB=75°，在同一平面内，将△ABC绕点A旋转到△AB’C’的位置，使CC’//AB，求∠BAB’的度数。
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列运动形式属于旋转的是（ ）
A.钟表上钟摆的摆动
B.投篮过程中球的运动
C.“神十”火箭升空的运动
D.传动带上物体位置的变化 -
科目： 来源： 题型：
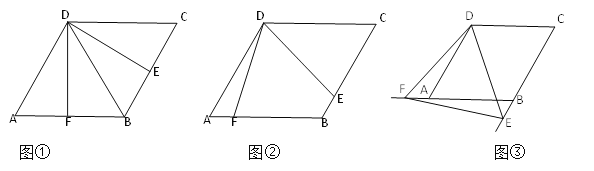
查看答案和解析>>【题目】如图，四边形ABCD是边长为2，一个锐角等于60°的菱形纸片，小芳同学将一个三角形纸片的一个顶点与该菱形顶点D重合，按顺时针方向旋转三角形纸片，使它的两边分别交CB、BA（或它们的延长线）于点E、F，
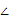EDF=60°，当CE=AF时，如图①小芳同学得出的结论是DE=DF。（1）继续旋转三角形纸片，当CE
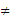AF时，如图②，小芳的结论是否成立？若成立，加以证明；若不成立，请说明理由。（2）再次旋转三角形纸片，当点E、F分别在CB、BA的延长线上时，如图③，请写出DE与DF的数量关系，并加以证明。
（3）连接EF，若△DEF的面积为y，CE=x，求y与x的关系式，并指出当x为何值时，y有最小值，最小值是多少？
相关试题
