【题目】如图,点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,下面四个结论正确的有________________.
①BP=CM;②△ABQ≌△CAP;③∠CMQ的度数不变,始终等于60°;④当第![]() 秒或第
秒或第![]() 秒时,△PBQ为直角三角形.
秒时,△PBQ为直角三角形.

参考答案:
【答案】②③④
【解析】∵点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点,点P从顶点A,点Q从顶点B同时出发,且它们的速度都为1cm/s,
∴AP=BQ,∠ABQ=∠CAP=60°,AB=CA,BP=CQ,
∴△ABQ≌△CAP.(即结论②成立);
∴∠BAQ=∠ACP,
∵∠CMQ=∠ACP+∠CAM,
∴∠CMQ=∠BAQ+∠CAM=∠CAP=60°.(即结论③成立);
又∵∠MQC>∠ABQ=60°,
∴∠MQC>∠CMQ,
∴MC>QC,即MC>BP.(即结论①不成立);
设t秒时,△BPQ是直角三角形,此时AP=BQ=t,BP=4-t,
(1)当∠PQB=90°,∵∠PBQ=60°,
∴∠BPQ=30°,
∴BQ=![]() PB,即
PB,即![]() ,解得:
,解得: ![]() ;
;
(2)当∠QPB=90°时,∵∠PBQ=60°,
∴∠PQB=30°,
∴BP=![]() BQ,即
BQ,即![]() ,解得:
,解得: ![]() .
.
结合(1)、(2)可得:当![]() 或
或![]() 时,△BPQ是直角三角形.(即结论④成立);
时,△BPQ是直角三角形.(即结论④成立);
综上所述,正确的结论是:②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为4,∠DAC的平分线交DC于点E,若点P,Q分别是AD和AE上的动点,则DQ+PQ的最小值是________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,抛物线y=ax2+3ax+c(a>0)与y轴交于点C,与X轴交于A、B两点,点A在点B左侧,点B的坐标为(1,0),OC=3OB.
(1)求抛物线对应的函数解析式;
(2)若点D是线段AC下方抛物线上的动点,求四边形ABCD面积的最大值。

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线y=mx+n(m,n为常数)经过点(0,﹣2)和(3,0),则关于x的方程mx+n=0的解为( )
A. x=0 B. x=1 C. x=﹣2 D. x=3
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)尺规作图:如图1,在四边形ABCD内找一点P,使得点P到AB、BC的距离相等,并且点P到点A、D的距离也相等.(不写作法,保留作图痕迹).
(2)如图2,在长度为1个单位长度的小正方形组成的正方形网格中,点A、B、C在小正方形的顶点上,①△ABC的面积为______.
②在图中画出与△ABC关于直线l成轴对称的△A1B1C1.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE,BC=DE.
(1)求证:∠ACD=∠B;
(2)若∠A=40°,求∠BCD的度数.
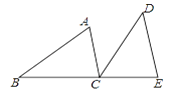
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠CAB=75°,在同一平面内,将△ABC绕点A旋转到△AB’C’的位置,使CC’//AB,求∠BAB’的度数。
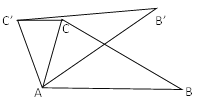
相关试题

