【题目】如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4 ![]() 且∠AFG=60°,GE=2BG,则折痕EF的长为( )
且∠AFG=60°,GE=2BG,则折痕EF的长为( ) 
A.1
B.![]()
C.2
D.![]()
参考答案:
【答案】C
【解析】解:由折叠的性质可知,DF=GF,HE=CE,GH=DC,∠DFE=∠GFE. ∵∠GFE+∠DFE=180°﹣∠AFG=120°,
∴∠GFE=60°.
∵AF∥GE,∠AFG=60°,
∴∠FGE=∠AFG=60°,
∴△GEF为等边三角形,
∴EF=GE.
∵∠FGE=60°,∠FGE+∠HGE=90°,
∴∠HGE=30°.
在Rt△GHE中,∠HGE=30°,
∴GE=2HE=CE,
∴GH= ![]() =
= ![]() HE=
HE= ![]() CE.
CE.
∵GE=2BG,
∴BC=BG+GE+EC=4EC.
∵矩形ABCD的面积为4 ![]() ,
,
∴4EC ![]() EC=4
EC=4 ![]() ,
,
∴EC=1,EF=GE=2.
故选C.
【考点精析】解答此题的关键在于理解矩形的性质的相关知识,掌握矩形的四个角都是直角,矩形的对角线相等,以及对翻折变换(折叠问题)的理解,了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为加强公路的节水意识,合理利用水资源,某市对居民用水实行阶梯水价,居民家庭每月用水量划分为两个阶梯,一、二阶梯用水的单价之比等于1:2,如图折线表示实行阶梯水价后每月水费y(元)与用水量x(m3)之间的函数关系,其中射线AB表示第二级阶梯时y与x之间的函数关系.

(1)写出点B的实际意义;
(2)求射线AB所在直线的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】若两个二次函数图象的顶点相同,开口大小相同,但开口方向相反,则称这两个二次函数为“对称二次函数”.
(1)请写出二次函数y=2(x﹣2)2+1的“对称二次函数”;
(2)已知关于x的二次函数y1=x2﹣3x+1和y2=ax2+bx+c,若y1﹣y2与y1互为“对称二次函数”,求函数y2的表达式,并求出当﹣3≤x≤3时,y2的最大值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,△ABC是等腰直角三角形,四边形ADEF是正方形,D、F分别在AB、AC边上,此时BD=CF,BD⊥CF成立.
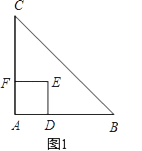
(1)当正方形ADEF绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.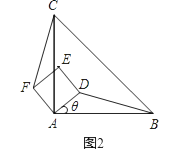
(2)当正方形ADEF绕点A逆时针旋转45°时,如图3,延长BD交CF于点G.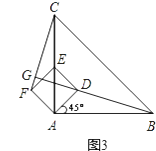
①求证:BD⊥CF;
②当AB=4,AD=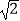 时,求线段BG的长.
时,求线段BG的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A(a,3),B(b,1)都在双曲线y=
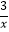 上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )
上,点C,D,分别是x轴,y轴上的动点,则四边形ABCD周长的最小值为( )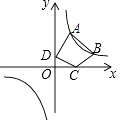
A.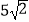
B.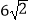
C.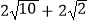
D.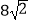
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c过点(﹣1,0),且对称轴为直线x=1,有下列结论: ①abc<0;②10a+3b+c>0;③抛物线经过点(4,y1)与点(﹣3,y2),则y1>y2;④无论a,b,c取何值,抛物线都经过同一个点(﹣
 ,0);⑤am2+bm+a≥0,其中所有正确的结论是 .
,0);⑤am2+bm+a≥0,其中所有正确的结论是 . 
-
科目: 来源: 题型:
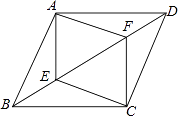
查看答案和解析>>【题目】如图,四边形ABCD是平行四边形,E,F是对角线BD上的两点,且BF=ED,求证:AE∥CF.
相关试题

