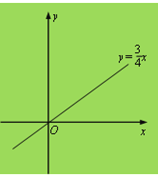
【题目】一次函数y=![]() x的图象如图所示,它与二次函数y=ax2-4ax+c的图象交于A、B两点(其中点A在点B的左侧),与这个二次函数图象的对称轴交于点C.
x的图象如图所示,它与二次函数y=ax2-4ax+c的图象交于A、B两点(其中点A在点B的左侧),与这个二次函数图象的对称轴交于点C.
(1)求点C的坐标;
(2)设二次函数图象的顶点为D.
①若点D与点C关于x轴对称,且△ACD的面积等于3,求此二次函数的关系式;
②若CD=AC,且△ACD的面积等于10,求此二次函数的关系式.
参考答案:
【答案】(1)点C(2, ![]() );(2)①y=
);(2)①y=![]() x2-
x2-![]() x; ②y=-
x; ②y=-![]() x2+2x+
x2+2x+![]() .
.
【解析】试题分析:(1)求得二次函数y=ax2-4ax+c对称轴为直线x=2,把x=2代入y=![]() x求得y=
x求得y=![]() ,即可得点C的坐标;(2)①根据点D与点C关于x轴对称即可得点D的坐标,并且求得CD的长,设A(m,
,即可得点C的坐标;(2)①根据点D与点C关于x轴对称即可得点D的坐标,并且求得CD的长,设A(m, ![]() m) ,根据S△ACD=3即可求得m的值,即求得点A的坐标,把A.D的坐标代入y=ax2-4ax+c得方程组,解得a、c的值即可得二次函数的表达式.②设A(m,
m) ,根据S△ACD=3即可求得m的值,即求得点A的坐标,把A.D的坐标代入y=ax2-4ax+c得方程组,解得a、c的值即可得二次函数的表达式.②设A(m, ![]() m)(m<2),过点A作AE⊥CD于E,则AE=2-m,CE=
m)(m<2),过点A作AE⊥CD于E,则AE=2-m,CE=![]() -
-![]() m,
m,
根据勾股定理用m表示出AC的长,根据△ACD的面积等于10可求得m的值,即可得A点的坐标,分两种情况:第一种情况,若a>0,则点D在点C下方,求点D的坐标;第二种情况,若a<0,则点D在点C上方,求点D的坐标,分别把A、D的坐标代入y=ax2-4ax+c即可求得函数表达式.
试题解析:(1)y=ax2-4ax+c=a(x-2)2-4a+c.∴二次函数图像的对称轴为直线x=2.
当x=2时,y=![]() x=
x=![]() ,∴C(2,
,∴C(2, ![]() ).
).
(2)①∵点D与点C关于x轴对称,∴D(2,- ![]() ),∴CD=3.
),∴CD=3.
设A(m, ![]() m) (m<2),由S△ACD=3,得
m) (m<2),由S△ACD=3,得![]() ×3×(2-m)=3,解得m=0,∴A(0,0).
×3×(2-m)=3,解得m=0,∴A(0,0).
由A(0,0)、 D(2,- ![]() )得
)得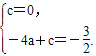 解得a=
解得a=![]() ,c=0.
,c=0.
∴y=![]() x2-
x2-![]() x.
x.
②设A(m, ![]() m)(m<2),过点A作AE⊥CD于E,则AE=2-m,CE=
m)(m<2),过点A作AE⊥CD于E,则AE=2-m,CE=![]() -
-![]() m,
m,
AC=![]() =
=![]() (2-m),
(2-m),
∵CD=AC,∴CD=![]() (2-m).
(2-m).
由S△ACD=10得![]() ×
×![]() (2-m)2=10,解得m=-2或m=6(舍去),∴m=-2.
(2-m)2=10,解得m=-2或m=6(舍去),∴m=-2.
∴A(-2,- ![]() ),CD=5.
),CD=5.
若a>0,则点D在点C下方,∴D(2,- ![]() ),
),
由A(-2,- ![]() )、D(2,-
)、D(2,- ![]() )得
)得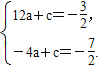 解得
解得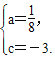
∴y=![]() x2-
x2-![]() x-3.
x-3.
若a<0,则点D在点C上方,∴D(2, ![]() ),
),
由A(-2,- ![]() )、D(2,
)、D(2, ![]() )得
)得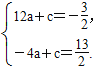 解得
解得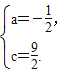
∴y=-![]() x2+2x+
x2+2x+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD内部有若干个点,用这些点以及正方形ABCD的顶点A、B、C、D把原正方形分割成一些三角形(互相不重叠):
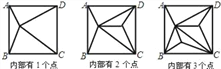
(1)填写下表:
正方形ABCD内点的个数
1
2
3
4
…
n
分割成的三角形的个数
4
6
…
(2)原正方形能否被分割成2008个三角形?若能,求此时正方形ABCD内部有多少个点?若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把四张形状大小完全相同的小正方形卡片(如图1)不重叠地放在一个底面为长方形(长为mcm,宽为ncm)的盒子的底部(如图2),盒子底面未被卡片覆盖的部分用阴影表示.则图2中两块阴影部分的周长和是( )

A. 4mcmB. 4ncmC. 2(m+n)cmD. 4(mn)cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校组织团员举行申奥成功宣传活动,从学校骑车出发,先上坡到达A地后,宣传8分钟;然后下坡到B地宣传8分钟返回,行程情况如图.若返回时,上、下坡速度仍保持不变,在A地仍要宣传8分钟,那么他们从B地返回学校用的时间是( )

A. 45.2分钟 B. 48分钟 C. 46分钟 D. 33分钟
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(1),一架长4米的梯子AB斜靠在与地面OM垂直的墙ON上,梯子与地面的倾斜角α为60°.
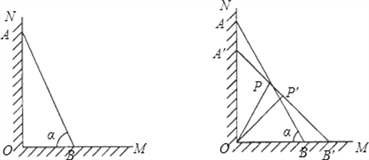
(1)求AO与BO的长;
(2)若梯子顶端A沿NO下滑,同时底端B沿OM向右滑行.如图(2),当A点下滑到A′点,B点向右滑行到B′点时,梯子AB的中点P也随之运动到P′点,若∠POP′=15°,试求AA′的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=ax2+bx+c的顶点为D(﹣1,2),与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则以下结论:①b2﹣4ac<0;②当x>﹣1时,y随x增大而减小;③a+b+c<0;④若方程ax2+bx+c﹣m=0没有实数根,则m>2; ⑤3a+c<0.其中正确结论的个数是( )

A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
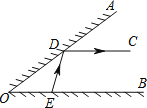
查看答案和解析>>【题目】如图,△AOB的边OA半面镜.∠AOB=36°,在OB边上有点E,从点E射出一束光线经平面镜反射后,反射光线DC恰好满足DC∥OB,已知入射光线、反射光线与半面镜的夹角相等,即∠ODE=∠ADC,求∠DEB的度数.
相关试题

