【题目】如图,点A和动点P在直线l上,点P关于点A的对称点为Q,以AQ为边作Rt△ABQ,使∠BAQ=90°,AQ:AB=3:4,作△ABQ的外接圆O.点C在点P右侧,PC=4,过点C作直线m⊥l,过点O作OD⊥m于点D,交AB右侧的圆弧于点E.在射线CD上取点F,使DF= ![]() CD,以DE,DF为邻边作矩形DEGF.设AQ=3x.
CD,以DE,DF为邻边作矩形DEGF.设AQ=3x. 
(1)用关于x的代数式表示BQ,DF.
(2)当点P在点A右侧时,若矩形DEGF的面积等于90,求AP的长.
(3)在点P的整个运动过程中, ①当AP为何值时,矩形DEGF是正方形?
②作直线BG交⊙O于点N,若BN的弦心距为1,求AP的长(直接写出答案).
参考答案:
【答案】
(1)解:在Rt△ABQ中,
∵AQ:AB=3:4,AQ=3x,
∴AB=4x,
∴BQ=5x,
∵OD⊥m,m⊥l,
∴OD∥l,
∵OB=OQ,
∴ ![]() =2x,
=2x,
∴CD=2x,
∴FD= ![]() =3x
=3x
(2)解:∵AP=AQ=3x,PC=4,
∴CQ=6x+4,
作OM⊥AQ于点M(如图1),

∴OM∥AB,
∵⊙O是△ABQ的外接圆,∠BAQ=90°,
∴点O是BQ的中点,
∴QM=AM= ![]() x
x
∴OD=MC= ![]() ,
,
∴OE= ![]() BQ=
BQ= ![]() ,
,
∴ED=2x+4,
S矩形DEGF=DFDE=3x(2x+4)=90,
解得:x1=﹣5(舍去),x2=3,
∴AP=3x=9
(3)解:①若矩形DEGF是正方形,则ED=DF,
I.点P在A点的右侧时(如图1)
∴2x+4=3x,解得:x=4,
∴AP=3x=12;
II.点P在A点的左侧时,
当点C在Q右侧,
0<x< ![]() 时(如图2),
时(如图2),

∵ED=4﹣7x,DF=3x,
∴4﹣7x=3x,解得:x= ![]() ,
,
∴AP= ![]() ;
;
当 ![]() ≤x<
≤x< ![]() 时(如图3),
时(如图3),

∵ED=4﹣7x,DF=3x,
∴4﹣7x=3x,解得:x= ![]() (舍去),
(舍去),
当点C在Q的左侧时,即x≥ ![]() (如图4),
(如图4),

DE=7x﹣4,DF=3x,
∴7x﹣4=3x,解得:x=1,
∴AP=3,
综上所述:当AP为12或 ![]() 或3时,矩形DEGF是正方形;
或3时,矩形DEGF是正方形;
②连接NQ,由点O到BN的弦心距为l,得NQ=2,
当点N在AB的左侧时(如图5),

过点B作BM⊥EG于点M,
∵GM=x,BM=x,
∴∠GBM=45°,
∴BM∥AQ,
∴AI=AB=4x,
∴IQ=x,
∴NQ= ![]() =2,
=2,
∴x=2 ![]() ,
,
∴AP=6 ![]() ;
;
当点N在AB的右侧时(如图6),

过点B作BJ⊥GE于点J,
∵GJ=x,BJ=4x,
∴tan∠GBJ= ![]() ,
,
∴AI=16x,∴QI=19x,
∴NQ= ![]() =2,
=2,
∴x= ![]() ,
,
∴AP= ![]() ,
,
综上所述:AP的长为6 ![]() 或
或 ![]() .
.
【解析】(1)由AQ:AB=3:4,AQ=3x,易得AB=4x,由勾股定理得BQ,再由中位线的性质得AH=BH= ![]() AB,求得CD,FD;(2)利用(1)的结论,易得CQ的长,作OM⊥AQ于点M(如图1),则OM∥AB,由垂径定理得QM=AM=
AB,求得CD,FD;(2)利用(1)的结论,易得CQ的长,作OM⊥AQ于点M(如图1),则OM∥AB,由垂径定理得QM=AM= ![]() x,由矩形性质得OD=MC,利用矩形面积,求得x,得出结论;(3)①点P在A点的右侧时(如图1),利用(1)(2)的结论和正方形的性质得2x+4=3x,得AP;点P在A点的左侧时,当点C在Q右侧,0<x<
x,由矩形性质得OD=MC,利用矩形面积,求得x,得出结论;(3)①点P在A点的右侧时(如图1),利用(1)(2)的结论和正方形的性质得2x+4=3x,得AP;点P在A点的左侧时,当点C在Q右侧,0<x< ![]() 时(如图2),4﹣7x=3x,解得x,易得AP;当
时(如图2),4﹣7x=3x,解得x,易得AP;当 ![]() 时(如图3),7﹣4x=3x,得AP;当点C在Q的左侧时,即x≥
时(如图3),7﹣4x=3x,得AP;当点C在Q的左侧时,即x≥ ![]() (如图4),同理得AP;②连接NQ,由点O到BN的弦心距为l,得NQ=2,当点N在AB的左侧时(如图5),过点B作BM⊥EG于点M,GM=x,BM=x,易得∠GBM=45°,BM∥AQ,易得AI=AB,求得IQ,由NQ得AP;当点N在AB的右侧时(如图6),过点B作BJ⊥GE于点J,由GJ=x,BJ=4x得tan∠GBJ=
(如图4),同理得AP;②连接NQ,由点O到BN的弦心距为l,得NQ=2,当点N在AB的左侧时(如图5),过点B作BM⊥EG于点M,GM=x,BM=x,易得∠GBM=45°,BM∥AQ,易得AI=AB,求得IQ,由NQ得AP;当点N在AB的右侧时(如图6),过点B作BJ⊥GE于点J,由GJ=x,BJ=4x得tan∠GBJ= ![]() ,利用(1)(2)中结论得AI=16x,QI=19x,解得x,得AP.
,利用(1)(2)中结论得AI=16x,QI=19x,解得x,得AP.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,CD⊥AB于点C,交半圆于点E,DF切半圆于点F.已知∠AEF=135°.

(1)求证:DF∥AB;
(2)若OC=CE,BF= ,求DE的长.
,求DE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】某农业观光园计划将一块面积为900m2的园圃分成A,B,C三个区域,分别种植甲、乙、丙三种花卉,且每平方米栽种甲3株或乙6株或丙12株.已知B区域面积是A区域面积的2倍.设A区域面积为x(m2).
(1)求该园圃栽种的花卉总株数y关于x的函数表达式.
(2)若三种花卉共栽种6600株,则A,B,C三个区域的面积分别是多少?
(3)若三种花卉的单价(都是整数)之和为45元,且差价均不超过10元,在(2)的前提下,全部栽种共需84000元.请写出甲、乙、丙三种花卉中,种植面积最大的花卉总价. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=﹣x2+6x交x轴正半轴于点A,顶点为M,对称轴MB交x轴于点B.过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.
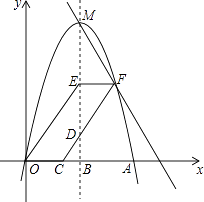
(1)求点A,M的坐标.
(2)当BD为何值时,点F恰好落在该抛物线上?
(3)当BD=1时
求直线MF的解析式,并判断点A是否落在该直线上.
(4)②延长OE交FM于点G,取CF中点P,连结PG,△FPG,四边形DEGP,四边形OCDE的面积分别记为S1 , S2 , S3 , 则S1:S2:S3= . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知E,F,G,H分别为正方形ABCD各边上的动点,且始终保持AE=BF=CG=DH,点M,N,P,Q分别是EH、EF、FG、HG的中点.当AE从小于BE的变化过程中,若正方形ABCD的周长始终保持不变,则四边形MNPQ的面积变化情况是( )

A.一直增大
B.一直减小
C.先增大后减小
D.先减小后增大 -
科目: 来源: 题型:
查看答案和解析>>【题目】在一堂关于“折纸问题”的数学综合实践探究课中,小明同学将一张矩形ABCD纸片,按如图进行折叠,分别在BC、AD两边上取两点E,F,使CE=AF,分别以DE,BF为对称轴将△CDE与△ABF翻折得到△C′DE与△A′BF,且边C′E与A′B交于点G,边A′F与C′D交于一点H.已知tan∠EBG=
 ,A′G=6,C′G=1,则矩形纸片ABCD的周长为 .
,A′G=6,C′G=1,则矩形纸片ABCD的周长为 . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸中,A,B,C三点都在小方格的顶点上(每个小方格的边长为1).

(1)在图甲中画一个以A,B,C为其中三个顶点的平行四边形,并求出它的周长.
(2)在图乙中画一个经过A,B,C三点的圆,并求出圆的面积.
相关试题

