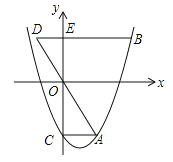
【题目】如图,抛物线![]() (m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(1)用含m的代数式表示BE的长.
(2)当m=![]() 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
参考答案:
【答案】(1)BE=2m;(2)点D在抛物线上;(3)①![]() ;②
;②![]() .
.
【解析】
试题分析:(1)根据A、C两点纵坐标相同,求出点A横坐标即可解决问题.
(2)求出点D坐标,然后判断即可.
(3)①首先根据EO=2FG,证明BG=2DE,列出方程即可解决问题.
②求出直线AE、BO的解析式,求出交点M的横坐标,列出方程即可解决问题.
试题解析:(1)∵C(0,﹣3),AC⊥OC,∴点A纵坐标为﹣3,y=﹣3时,![]() ,解得x=0或m,∴点A坐标(m,﹣3),∴AC=m,∴BE=2AC=2m.
,解得x=0或m,∴点A坐标(m,﹣3),∴AC=m,∴BE=2AC=2m.
(2)点D在抛物线上.理由如下:
∵m=![]() ,∴点A坐标(
,∴点A坐标(![]() ,﹣3),∴直线OA为
,﹣3),∴直线OA为![]() ,∴抛物线解析式为
,∴抛物线解析式为![]() ,∴点B坐标(
,∴点B坐标(![]() ,3),∴点D纵坐标为3,对于函数
,3),∴点D纵坐标为3,对于函数![]() ,当y=3时,x=
,当y=3时,x=![]() ,∴点D坐标(
,∴点D坐标(![]() ,3).∵对于函数
,3).∵对于函数![]() ,x=
,x=![]() 时,y=3,∴点D在抛物线上;
时,y=3,∴点D在抛物线上;
(3)①∵∠ACE=∠CEG=∠EGA=90°,∴四边形ECAG是矩形,∴EG=AC=BG,∵FG∥OE,∴OF=FB,∵EG=BG,∴EO=2FG,∵![]() DEEO=
DEEO=![]() GBGF,∴BG=2DE,∵DE∥AC,∴
GBGF,∴BG=2DE,∵DE∥AC,∴![]() =
=![]() ,∵点B坐标(2m,
,∵点B坐标(2m,![]() ),∴OC=2OE,∴3=2(
),∴OC=2OE,∴3=2(![]() ),∵m>0,∴m=
),∵m>0,∴m=![]() .
.
②∵A(m,﹣3),B(2m,![]() ),E(0,
),E(0,![]() ),∴直线AE解析式为
),∴直线AE解析式为![]() ,直线OB解析式为
,直线OB解析式为![]() ,由
,由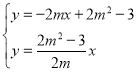 消去y得到
消去y得到![]() ,解得x=
,解得x=![]() ,∴点M横坐标为
,∴点M横坐标为![]() ,∵△AMF的面积=△BFG的面积,∴
,∵△AMF的面积=△BFG的面积,∴![]() ,整理得到:
,整理得到:![]() ,∵m>0,∴m=
,∵m>0,∴m=![]() .故答案为:
.故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=(a﹣1)x2﹣x+a2﹣1 的图象经过原点,则a的值为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解刚生产的10 000台电视机的寿命情况,从中抽取100台电视机进行实验,这个问题中的样本容量是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
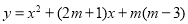 (m为常数,﹣1≤m≤4).A(﹣m﹣1,
(m为常数,﹣1≤m≤4).A(﹣m﹣1,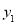 ),B(
),B(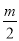 ,
,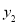 ),C(﹣m,
),C(﹣m,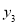 )是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.
)是该抛物线上不同的三点,现将抛物线的对称轴绕坐标原点O逆时针旋转90°得到直线a,过抛物线顶点P作PH⊥a于H.(1)用含m的代数式表示抛物线的顶点坐标;
(2)若无论m取何值,抛物线与直线y=x﹣km(k为常数)有且仅有一个公共点,求k的值;
(3)当1<PH≤6时,试比较
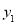 ,
,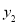 ,
,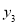 之间的大小.
之间的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我校九年级(1)班所有学生参加2015年初中毕业生升学体育测试,根据测试评分标准,将他们的成绩进行统计后分为A、B、C、D四等,并绘制成如图所示的条形统计图和扇形统计图(未完成),请结合图中所给信息解答下列问题:
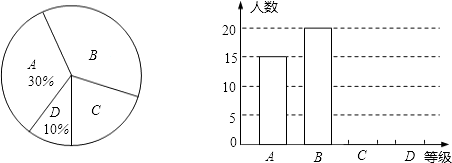
(1)九年级(1)班参加体育测试的学生有人;
(2)将条形统计图补充完整;
(3)在扇形统计图中,等级B部分所占的百分比是 , 等级C对应的圆心角的度数为;
(4)若该校九年级学生共有550人参加体育测试,估计达到A级和B级的学生共有人. -
科目: 来源: 题型:
查看答案和解析>>【题目】直角坐标系第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,试求x+2y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是由一些火柴棒搭成的图案:
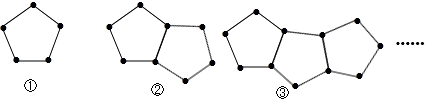
(1)摆第①个图案用根火柴棒,摆第②个图案用根火柴棒,摆第③个图案用根火柴棒.
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?
(3)计算一下摆121根火柴棒时,是第几个图案?
相关试题

