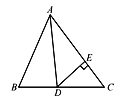
【题目】如图所示,在△ABC中,已知AD是角平分线,∠B=62°,∠C=58°.
(1)求∠ADB的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
参考答案:
【答案】(1)880(2)600 .
【解析】试题分析:⑴由题意易得∠BAC=60°,所以∠ BAD=30°,从而得到∠ ADB=88°.
⑵由⑴可知∠DAE=30°,所以∠ ADE=60°.
试题解析:⑴在△ABC中,∵∠B=62°,∠C=58°,∴ ∠BAC=60°.
又∵ AD是角平分线,∴∠BAD=∠CAD=30°.
在△ ABD中,∵ ∠ B=62°,∠ BAD=30°,∴ ∠ ADB=88°.
⑵在△ADE中,∵∠CAD=30°,∠AED=90°,∴∠ADE=60°.
-
科目: 来源: 题型:
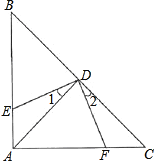
查看答案和解析>>【题目】如图:△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点,DE⊥DF.
(1)∠1=∠2吗?为什么?
(2)△ADE与△CDF全等吗?为什么?
(3)若AB=8cm,求四边形AEDF的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
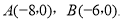 点
点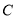 在
在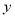 轴的正半轴上,
轴的正半轴上,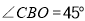 ,
,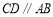 ,
,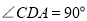 .点
.点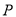 从点
从点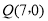 出发,沿
出发,沿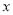 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为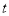 秒.
秒.(1)点
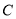 的坐标是 ;
的坐标是 ;(2)当
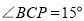 时,求
时,求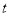 的值;
的值;(3)以点
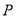 为圆心,
为圆心,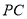 为半径的
为半径的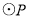 随点
随点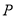 的运动而变化,当
的运动而变化,当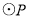 与四边形
与四边形 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求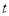 的值.
的值.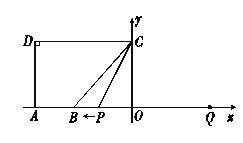
-
科目: 来源: 题型:
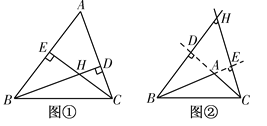
查看答案和解析>>【题目】(1)如图①,△ABC是锐角三角形,高BD,CE相交于点H,找出∠BHC和∠A之间存在何种等量关系;并证明你的结论;
(2)如图②,若△ABC是钝角三角形,∠A>90°,高BD,CE所在的直线相交于点H,请你判断此时(1)中的等量关系是否仍然成立?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列几组数据能作为直角三角形的三边长的是( )
A. 2,3,4 B. 5,3,4 C. 4,6,9 D. 5,11,13
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班抽取6名同学参加体能测试,成绩如下:80,90,75,75,80,80.下列表述错误的是( )
A. 众数是80 B. 中位数是75 C. 平均数是80 D. 极差是15
-
科目: 来源: 题型:
查看答案和解析>>【题目】在2014年8月南京青奥会前夕,某体育用品店销售一批青奥会纪念品,平均每天可销售20件,每件赢利40元。为了扩大销售,该体育用品店决定采取适当降价措施。经调查发现,如果该青奥会纪念品每降价1元,该店平均每天可多售出2件。求:
(1)若该家体育用品店平均每天要赢利1200元,则这批青奥会纪念品应降价多少元?
(2)用配方法说明,每件青奥会纪念品降价多少元时,该家体育用品店平均每天赢利最多,最多是多少?
相关试题

