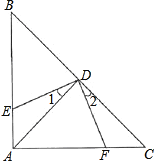
【题目】如图:△ABC中,∠BAC=90°,AB=AC,点D是斜边BC的中点,DE⊥DF.
(1)∠1=∠2吗?为什么?
(2)△ADE与△CDF全等吗?为什么?
(3)若AB=8cm,求四边形AEDF的面积.
参考答案:
【答案】(1)相等,理由见解析;(2)全等,理由见解析;(3)16平方厘米.
【解析】试题分析:(1)利用公共角证明∠1=∠2.
(2)利用直角三角形斜边中线是斜边一半得到AD=CD,∠C=∠DAC, ∠1=∠2,利用ASA证明
△ADE与△CDF全等.
(3)利用(2)的结论,割补法,四边形面积恰好是等腰三角形面积一半.
(1)∵AB=AC,D是BC的中点,
∴∠ADC=90 ,
∴∠2+∠ADF=90,
∵DE⊥DF ,
∴∠1+∠ADF=90,
∴∠1=∠2 .
(2) ∵△ABC是等腰直角三角形,
∴∠C=45,
∵AB=AC,D是BC的中点.
∴∠DAC=∠DAE=45°,
∴DA=DC,
在△ADE与△CDF中,
∠EAD=∠C=45 , DA=DC , ∠1=∠2,
∴△ADE≌△CDF.
(3)由(2)△ADE≌△CDF,
∴S△AED=S△CDF,
∵S四边形AEDF=S△ADE+S△ADF,
∴S四边形AEDF=S△CDF+S△ADF =S△ADC,
= ![]() S△ABC,,
S△ABC,,
= ![]() ×8×8=16(㎝2).
×8×8=16(㎝2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点(4,-5)关于原点的对称点的坐标是________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题是假命题的是( )
A. 平行四边形的对边相等 B. 四条边都相等的四边形是菱形
C. 矩形的两条对角线互相垂直 D. 等腰梯形的两条对角线相等
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,AC=CD,∠B=∠E=90°,AC⊥CD,则不正确的结论是( )
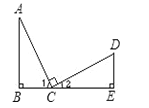
A. ∠1=∠2 B. ∠A =∠2 C. △ABC≌△CED D. ∠A与∠D互为余角
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 点
点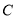 在
在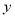 轴的正半轴上,
轴的正半轴上,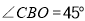 ,
,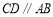 ,
,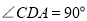 .点
.点 从点
从点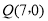 出发,沿
出发,沿 轴向左以每秒1个单位长的速度运动,运动时间为
轴向左以每秒1个单位长的速度运动,运动时间为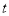 秒.
秒.(1)点
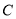 的坐标是 ;
的坐标是 ;(2)当
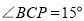 时,求
时,求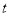 的值;
的值;(3)以点
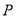 为圆心,
为圆心,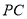 为半径的
为半径的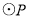 随点
随点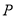 的运动而变化,当
的运动而变化,当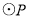 与四边形
与四边形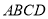 的边(或边所在的直线)相切时,求
的边(或边所在的直线)相切时,求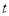 的值.
的值.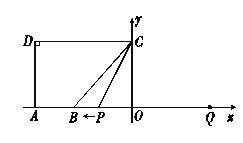
-
科目: 来源: 题型:
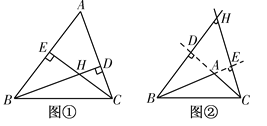
查看答案和解析>>【题目】(1)如图①,△ABC是锐角三角形,高BD,CE相交于点H,找出∠BHC和∠A之间存在何种等量关系;并证明你的结论;
(2)如图②,若△ABC是钝角三角形,∠A>90°,高BD,CE所在的直线相交于点H,请你判断此时(1)中的等量关系是否仍然成立?并说明理由.
-
科目: 来源: 题型:
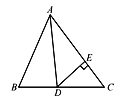
查看答案和解析>>【题目】如图所示,在△ABC中,已知AD是角平分线,∠B=62°,∠C=58°.
(1)求∠ADB的度数;
(2)若DE⊥AC于点E,求∠ADE的度数.
相关试题

