【题目】平面内的两条直线有相交和平行两种位置关系.
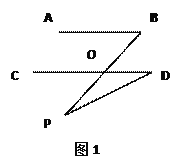
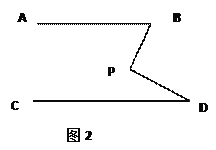
(1)AB∥CD.如图1,点P在AB,CD外部时,由AB∥CD,有∠B=∠BOD.又因为∠BOD是△POD的外角,故∠BOD=∠BPD +∠D ,得∠BPD=∠B-∠D.如图2,将点P移到AB,CD内部,以上结论是否成立?若不成立,则∠BPD,∠B,∠D之间有何数量关系?请证明你的结论.
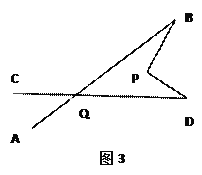
(2)在图2中,将直线AB绕点B按逆时针方向旋转一定角度交直线CD于点Q,如图3,则∠BPD,∠B,∠D,∠BQD之间有何数量关系?说明理由.
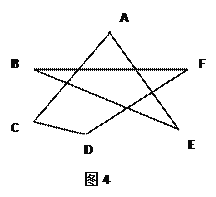
(3)根据(2)的结论,求图4中∠A+∠B+∠C+∠D+∠E+∠F的度数.
参考答案:
【答案】(1)不成立,∠BPD=∠B+∠D.
(2) ∠BPD=∠B+∠D+∠BQD.
(3) 360°
【解析】【试题分析】(1)利用两直线平行,内错角相等,得:PE//AB,则![]() ;利用平行线的传递性,得:PE//AB,AB//CD,所以PE//CD,再次利用利用两直线平行,内错角相等,得:PE//CD,则
;利用平行线的传递性,得:PE//AB,AB//CD,所以PE//CD,再次利用利用两直线平行,内错角相等,得:PE//CD,则![]() ,利用等量代换得:∠BPD=
,利用等量代换得:∠BPD=![]() =∠B+∠D.即∠BPD=∠B+∠D.
=∠B+∠D.即∠BPD=∠B+∠D.
(2)利用三角形的外角等于不相邻的两个内角和,得![]() ,再利用角度转化即可.即
,再利用角度转化即可.即![]() =
= ![]() .
.
(3)利用转化的思想,利用外角的性质,将6个角的和转化为四边形的内角和,即360°.
【试题解析】
(1)不成立,∠BPD=∠B+∠D.
理由:如图,作PE//AB,则![]() ,因为AB//CD,所以PE//CD,则
,因为AB//CD,所以PE//CD,则![]() ,所以∠BPD=
,所以∠BPD=![]() =∠B+∠D.即∠BPD=∠B+∠D.
=∠B+∠D.即∠BPD=∠B+∠D.
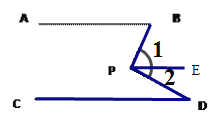
(2)作射线QP, ![]() ,则
,则![]() =
= ![]() .
.
即: ![]() =
= ![]() .
.
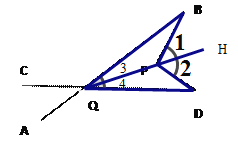
(3)由题意得: ![]() ,得∠A+∠B+∠C+∠D+∠E+∠F=∠C+∠D+
,得∠A+∠B+∠C+∠D+∠E+∠F=∠C+∠D+![]() =360°.
=360°.

-
科目: 来源: 题型:
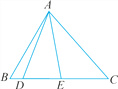
查看答案和解析>>【题目】如图,图中共有_______个三角形,以AD为边的三角形有_________________,以E为顶点的三角形有___________,∠ADB是______的内角,△ADE的三个内角分别是________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC≌△DEF,AB=DE,∠A=70°,∠E=30°,则∠F的度数为 ( )
A、 80° B、 70° C、 30 ° D、 100°
-
科目: 来源: 题型:
查看答案和解析>>【题目】五个有理数的积为负数,则这五个数中正因数的个数是 ( )
A.2个
B.1,3或5
C.0,2或4
D.无法确定 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在一次军事演习中,蓝方在一条东西走向的公路上的A处朝正南方向撤退,红方在公路上的B处沿南偏西60°方向前进实施拦截,红方行驶1000米到达C处后,因前方无法通行,红方决定调整方向,再朝南偏西45°方向前进了相同的距离,刚好在D处成功拦截蓝方,求拦截点D处到公路的距离(结果不取近似值).

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个点到圆的最小距离为6cm,最大距离为9cm,则该圆的半径是( )
A.1.5cm
B.7.5cm
C.1.5cm或7.5cm
D.3cm或15cm -
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,把△ABC纸片沿DE折叠,使点A落在四边形BCED内部点A′的位置.通过计算我们知道:2∠A=∠1+∠2.请你继续探索:
(1)如果把△ABC纸片沿DE折叠,使点A落在四边形BCED外部点A′的位置,如图②所示.此时∠A与∠1、∠2之间存在什么样的关系?并说明理由.
(2)如果把四边形ABCD沿EF折叠,使点A、D分别落在四边形BCFE内部点A′、D′的位置,如图③所示.你能求出∠A′、∠D′、∠1 与∠2之间的关系吗?并说明理由.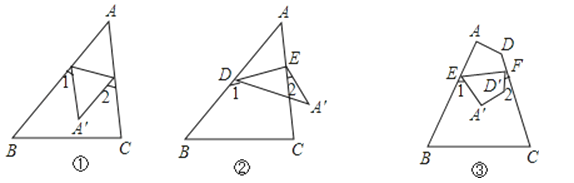
相关试题

