【题目】如图,抛物线经过A(﹣1,0),B(5,0),C(0,- ![]() )三点.
)三点.
(1)求抛物线的解析式;
(2)在抛物线的对称轴上有一点P,使PA+PC的值最小,求点P的坐标;
(3)点M为x轴上一动点,在抛物线上是否存在一点N,使以A,C,M,N四点构成的四边形为平行四边形?若存在,求点N的坐标;若不存在,请说明理由.
参考答案:
【答案】
(1)
解:设抛物线的解析式为y=ax2+bx+c(a≠0),
∵A(﹣1,0),B(5,0),C(0,- ![]() )三点在抛物线上,
)三点在抛物线上,
∴ 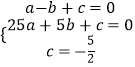 ,
,
解得 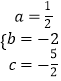 .
.
∴抛物线的解析式为:y= ![]() x2﹣2x﹣
x2﹣2x﹣ ![]() ;
;
(2)
解:∵抛物线的解析式为:y= ![]() x2﹣2x﹣
x2﹣2x﹣ ![]() ,
,
∴其对称轴为直线x=﹣ ![]() =﹣
=﹣ ![]() =2,
=2,
连接BC,如图1所示,
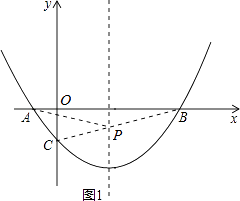
∵B(5,0),C(0,﹣ ![]() ),
),
∴设直线BC的解析式为y=kx+b(k≠0),
∴ 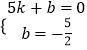 ,
,
解得 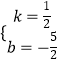 ,
,
∴直线BC的解析式为y= ![]() x﹣
x﹣ ![]() ,
,
当x=2时,y=1﹣ ![]() =﹣
=﹣ ![]() ,
,
∴P(2,﹣ ![]() );
);
(3)
解:存在.
如图2所示,
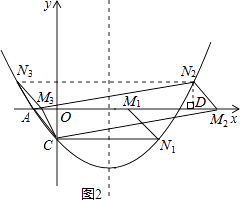
①当点N在x轴下方时,
∵抛物线的对称轴为直线x=2,C(0,﹣ ![]() ),
),
∴N1(4,﹣ ![]() );
);
②当点N在x轴上方时,
如图,过点N2作N2D⊥x轴于点D,
在△AN2D与△M2CO中,
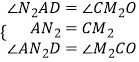
∴△AN2D≌△M2CO(ASA),
∴N2D=OC= ![]() ,即N2点的纵坐标为
,即N2点的纵坐标为 ![]() .
.
∴ ![]() x2﹣2x﹣
x2﹣2x﹣ ![]() =
= ![]() ,
,
解得x=2+ ![]() 或x=2﹣
或x=2﹣ ![]() ,
,
∴N2(2+ ![]() ,
, ![]() ),N3(2﹣
),N3(2﹣ ![]() ,
, ![]() ).
).
综上所述,符合条件的点N的坐标为(4,﹣ ![]() ),(2+
),(2+ ![]() ,
, ![]() )或(2﹣
)或(2﹣ ![]() ,
, ![]() ).
).
【解析】本题考查的是二次函数综合题,涉及到用待定系数法求一次函数与二次函数的解析式、平行四边的判定与性质、全等三角形等知识,在解答(3)时要注意进行分类讨论.(1)设抛物线的解析式为y=ax2+bx+c(a≠0),再把A(﹣1,0),B(5,0),C(0,- ![]() )三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.
)三点代入求出a、b、c的值即可;(2)因为点A关于对称轴对称的点B的坐标为(5,0),连接BC交对称轴直线于点P,求出P点坐标即可;(3)分点N在x轴下方或上方两种情况进行讨论.
【考点精析】本题主要考查了确定一次函数的表达式和平行四边形的判定与性质的相关知识点,需要掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;若一直线过平行四边形两对角线的交点,则这条直线被一组对边截下的线段以对角线的交点为中点,并且这两条直线二等分此平行四边形的面积才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果将四根木条首尾相连,在相连处用螺钉连接,就能构成一个平面图形.

(1)若固定三根木条AB,BC,AD不动,AB=AD=2cm,BC=5cm,如图,量得第四根木条CD=5cm,判断此时∠B与∠D是否相等,并说明理由.
(2)若固定一根木条AB不动,AB=2cm,量得木条CD=5cm,如果木条AD,BC的长度不变,当点D移到BA的延长线上时,点C也在BA的延长线上;当点C移到AB的延长线上时,点A、C、D能构成周长为30cm的三角形,求出木条AD,BC的长度. -
科目: 来源: 题型:
查看答案和解析>>【题目】根据直角三角形的判定的知识解决下列问题
(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知抛物线y=x2+bx+c过A,B,C三点,点A的坐标是(3,0),点C的坐标是(0,﹣3),动点P在抛物线上.

(1)b= , c= , 点B的坐标为;(直接填写结果)
(2)是否存在点P,使得△ACP是以AC为直角边的直角三角形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由;
(3)过动点P作PE垂直y轴于点E,交直线AC于点D,过点D作x轴的垂线.垂足为F,连接EF,当线段EF的长度最短时,求出点P的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,AD是△ABC的中线,∠ADC=45°,把△ADC沿AD对折,使点C落在点C的位置,则图中的一个等腰直角三角形是( )

A.△ADC′
B.△BDC′
C.△ADC
D.不存在 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知点E、F分别是AD、CE边上的中点,且S△BEF=4cm2 , 则S△ABC的值为( )
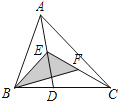
A.1cm2
B.2cm2
C.8cm2
D.16cm2 -
科目: 来源: 题型:
查看答案和解析>>【题目】工人师傅要将边长为4m和3m的平行四边形框架固定,现有下列长度的木棒,在木棒的两端钉上达到固定平行四边形的目的,不符合要求的是( )
A.2m
B.3m
C.4m
D.8m
相关试题

