【题目】根据直角三角形的判定的知识解决下列问题
(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°;
(2)如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明.
参考答案:
【答案】
(1)
证明:由旋转的性质知:BP=BQ、PA=QC,∠ABP=∠CBQ;
∵△ABC是等边三角形,
∴∠ABC=60°,即∠CBP+∠ABP=60°;
∵∠ABP=∠CBQ,
∴∠CBP+∠CBQ=60°,即∠PBQ=60°;
又∵BP=BQ,∴△BPQ是等边三角形;
∴BP=PQ;
∵PA2+PB2=PC2,即PQ2+QC2=PC2;
∴△PQC是直角三角形,且∠PQC=90°
(2)
解:PA2+2PB2=PC2;理由如下:
同(1)可得:△PBQ是等腰直角三角形,则PQ= ![]() PB,即PQ2=2PB2;
PB,即PQ2=2PB2;
由旋转的性质知:PA=QC;
在△PQC中,若∠PQC=90°,则PQ2+QC2=PC2,即PA2+2PB2=PC2;
故当PA2+2PB2=PC2时,∠PQC=90°.
【解析】(1)由旋转的性质可得到的条件是:①BP=BQ、PA=QC,②∠ABP=∠CBQ;
由②可证得∠PBQ=∠CBP+∠CBQ=∠CBP+∠ABP=∠ABC=60°,联立BP=BQ,即可得到△BPQ是等边三角形的结论,则BP=PQ;将等量线段代换后,即可得出PQ2+QC2=PC2,由此可证得∠PQC=90°;(2)由(1)的解题思路知:△PBQ是等腰Rt△,则PQ2=2PB2,其余过程同(1),只不过所得结论稍有不同.此题考查了等边三角形、等腰直角三角形的性质,旋转的性质,直角三角形的判定及勾股定理的应用等知识,能够正确的判断出△BPQ的形状,从而得到BP、PQ的数量关系,是解答此题的关键.
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识,掌握等边三角形的三个角都相等并且每个角都是60°,以及对勾股定理的逆定理的理解,了解如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13nmile的A,B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120nmile,乙巡逻艇每小时航行50nmile,航向为北偏西40°,问:甲巡逻艇的航向是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】去年以来,我国中东部地区持续出现雾霾天气.我市某记者为了了解“雾霾天气的主要成因”,随机调查了部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计表:
组别
观点
频数
A
大气气压低,空气不流动
120
B
地面灰尘多,空气湿度低
M
C
汽车尾气排放
N
D
工厂造成的污染
180
E
其它
90
请根据图表中提供的信息解答下列问题:
(1)填空:m、n等于多少?扇形统计图中E组所占百分比为多少?
(2)若该市人口约有75万人,请你估计其中持D组“观点”的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人持C组“观点”的概率是多少?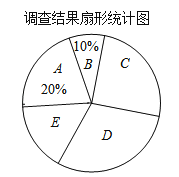
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级在母亲节倡议“感恩母亲,做点家务”活动.为了解同学们在母亲节的周末做家务情况,年级随机调查了部分同学,并用得到的数据制成如下不完整的统计表.
(1)统计表中的
 ,
, ;
;(2)被调查同学做家务时间的中位数是 小时,平均数是 小时;
(3)年级要组织一次"感恩母亲“的主题级会,级长想从报名的4位同学中随机抽取2位同学在会上谈体会.据统计,报名的4人分别是母亲节的周末做家务1小时的1人、做家务1.5小时的2人、做家务2小时的1人.请你算算选上的2位同学恰好是一位做家务2小时和一位做家务1.5小时的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】2015年全国两会民生话题成为社会焦点,安庆市记者为了了解百姓“两会民生话题”的聚焦点,随机调查了安庆市部分市民,并对调查结果进行整理,绘制了如图所示的不完整的统计图表.
组别
焦点话题
频数(人数)
A
食品安全
80
B
教育医疗
m
C
就业养老
n
D
生态环保
120
E
其他
60
请根据图表中提供的信息解答下列问题:
(1)填空:m、n等于多少?扇形统计图中E组所占的百分比为多少?
(2)安庆市人口现有6200万人,请你估计其中关注D组话题的市民人数;
(3)若在这次接受调查的市民中,随机抽查一人,则此人关注C组话题的概率是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD的四条边长分别为54cm,48cm,45cm,63cm,另一个和它相似的四边形最短边长为15cm,则这个四边形的最长边为( ).
A.18cm
B.16cm
C.21cm
D.24cm -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一矩形长20cm,宽为10cm,另一与它相似的矩形的一边长为10cm,求另一边长.
相关试题

