【题目】如图1,在△ABC中,AB=AC,点D是BC边上一点(不与点B、C重合),以AD为边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE,设∠BAC=α,∠BCE=β.
(1)线段BD、CE的数量关系是________;并说明理由;
(2)探究:当点D在BC边上移动时,α,β之间有怎样的数量关系?请说明理由;
(3)如图2,若∠BAC=90°,CE与BA的延长线交于点F.求证:EF=DC.


参考答案:
【答案】(1)BD=CE,理由见解析;(2)α+β=180°,理由见解析;(3)见解析.
【解析】
(1)首先求出∠BAD=∠CAE,再利用SAS得出△ABD≌△ACE即可得BD=CE;
(2)利用△ABD≌△ACE,推出∠BAC+∠BCE=180°,根据三角形内角和定理求出即可;
(3)利用△ABD≌△ACE,可得∠B=∠ACE,由∠BAC=90°,AB=AC得∠B=∠ACE=∠ACB=45°,可证出△BCF是等腰直角三角形,则BC=FC,即可得出结论.
(1)BD=CE.
证明:∵∠BAC=∠DAE,
∴∠BAD=∠CAE,
∵在△ABD和△ACE中,
 ,
,
∴△ABD≌△ACE(SAS)
∴BD=CE;
(2)α+β=180°
理由:∵△ABD≌△ACE,
∴∠B=∠ACE,
∴∠BCE=∠ACB+∠ACE=∠ACB+∠B,
∵∠BAC+∠B+∠ACB=180°,
∴∠BAC+∠BCE=180°,
即α+β=180°;
(3)∵△ABD≌△ACE,
∴∠B=∠ACE,BD=CE,
∵∠BAC=90°,AB=AC,
∴∠B=∠ACE=∠ACB=45°,
∴△BCF是等腰直角三角形,
∴BC=FC,
∴BC-BD=FC-CE,即EF=DC.
故答案为:(1)BD=CE,理由见解析;(2)α+β=180°,理由见解析;(3)见解析.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在菱形ABCD 中,点E,O,F分别是边AB,AC,AD的中点,连接CE、CF、OE、OF.当AB与BC满足___________条件时,四边形AEOF正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,下列条件不能判定四边形ABCD是矩形的是( )

A.∠DAB=∠ABC=∠BCD=90°B.AB∥CD,AB=CD,AB⊥AD
C.AO=BO,CO=DOD.AO=BO=CO=DO
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,正方形A1B1C1D1、D1 E1E2B2、A2B2 C2D2、D2 E3E4B3……按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3……在x轴上,已知正方形A1B1C1D1的边长为l,∠B1C1O= 60°, B1C1∥B2C2∥B3C3……,则正方形A2017B2017 C2017 D2017的边长是( )

A. (
 )2016 B. (
)2016 B. ( )2017 C. (
)2017 C. ( )2016 D. (
)2016 D. ( )2017
)2017 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,各内角的平分线相交于点E,F,G,H.
(1)求证:四边形EFGH是矩形;
(2)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分已知关于x的一元二次方程(m-2)x2+(2m+1)x+m=0有两个实数根x1,x2.
(1)求m的取值范围.
(2)若|x1|=|x2|,求m的值及方程的根.
-
科目: 来源: 题型:
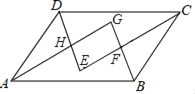
查看答案和解析>>【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.

相关试题

