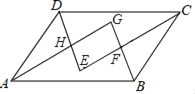
【题目】已知:如图,平行四边形ABCD,对角线AC与BD相交于点E,点G为AD的中点,连接CG,CG的延长线交BA的延长线于点F,连接FD.
(1)求证:AB=AF;
(2)若AG=AB,∠BCD=120°,判断四边形ACDF的形状,并证明你的结论.

参考答案:
【答案】(1)证明见解析;(2)结论:四边形ACDF是矩形.理由见解析.
【解析】
(1)只要证明AB=CD,AF=CD即可解决问题;
(2)结论:四边形ACDF是矩形.根据对角线相等的平行四边形是矩形判断即可;
(1)证明:∵四边形ABCD是平行四边形,
∴BE∥CD,AB=CD,
∴∠AFC=∠DCG,
∵GA=GD,∠AGF=∠CGD,
∴△AGF≌△DGC,
∴AF=CD,
∴AB=CF.
(2)解:结论:四边形ACDF是矩形.
理由:∵AF=CD,AF∥CD,
∴四边形ACDF是平行四边形,
∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD=120°,
∴∠FAG=60°,
∵AB=AG=AF,
∴△AFG是等边三角形,
∴AG=GF,
∵△AGF≌△DGC,
∴FG=CG,∵AG=GD,
∴AD=CF,
∴四边形ACDF是矩形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在△ABC中,AB=AC,点D是BC边上一点(不与点B、C重合),以AD为边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE,设∠BAC=α,∠BCE=β.
(1)线段BD、CE的数量关系是________;并说明理由;
(2)探究:当点D在BC边上移动时,α,β之间有怎样的数量关系?请说明理由;
(3)如图2,若∠BAC=90°,CE与BA的延长线交于点F.求证:EF=DC.


-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,各内角的平分线相交于点E,F,G,H.
(1)求证:四边形EFGH是矩形;
(2)若AB=6,BC=4,∠DAB=60°,求四边形EFGH的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分已知关于x的一元二次方程(m-2)x2+(2m+1)x+m=0有两个实数根x1,x2.
(1)求m的取值范围.
(2)若|x1|=|x2|,求m的值及方程的根.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,AE⊥BC于点E,延长BC至点F使CF=BE,连结AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形ABCD在平面直角坐标系中,点A(1,8),B(1,6),C(7,6).
(1)请直接写出D点的坐标.
(2)连接OB,OD,BD,请求出三角形OBD的面积.
(3)若长方形ABCD以每秒1个单位长度的速度向下运动,当边BC与x轴重合时,停止运动,设运动的时间为t秒,t为多少时,三角形OBD的面积等于长方形ABCD的面积的
 ?
?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,DB∥AC,且DB=
 AC,E是AC的中点,
AC,E是AC的中点,(1)求证:BC=DE;
(2)连接AD、BE,若要使四边形DBEA是矩形,则给△ABC添加什么条件,为什么?

相关试题

