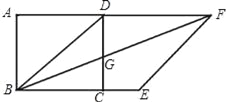
【题目】如图,正方形ABCD中,以对角线BD为边作菱形BDFE,使B,C,E三点在同一直线上,连接BF,交CD于点G.
(1)求证:CG=CE;
(2)若正方形边长为4,求菱形BDFE的面积.
参考答案:
【答案】(1)证明见解析;(2)16![]() .
.
【解析】
(1)连接DE,则DE⊥BF,可得∠CDE=∠CBG,根据BC=DC,∠BCG=∠DCE,可证△BCG≌△DCE,可证CG=CE;
(2)已知正方形的边长可以证明BD,即BE,根据BE,DC即可求菱形BDFE的面积.
解(1)证明:连接DE,则DE⊥BF,
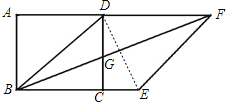
∵∠CBG+∠BED=90°,∠CBG+∠CGB=90°,∠CGB=∠BED
又∵BC=DC,∠BCG=∠DCE,
∴△BCG≌△DCE(AAS),
∴CG=CE,
(2)正方形边长BC=4,则BD=BE=![]() ,DC=4,菱形BDFE的面积为S=4
,DC=4,菱形BDFE的面积为S=4![]() ×4=16
×4=16![]() .
.
答:菱形BDFE的面积为16![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,D是BC上一点,△ABC∽△ADE,
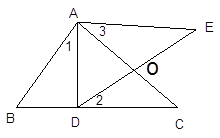
求证:∠1=∠2=∠3 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两座城市相距100千米,现计划在两城市间修筑一条高速公路(即线段AB).经测量,森林保护区中心P点既在A城市的北偏东30°的方向上,又在B城市的南偏东45°的方向上.已知森林保护区的范围是以P为圆心,35千米为半径的圆形区域内.请问:计划修筑的这条高速公路会不会穿越森林保护区?请通过计算说明.(参考数据:
 ≈1.732,
≈1.732,  ≈1.414)
≈1.414)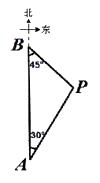
-
科目: 来源: 题型:
查看答案和解析>>【题目】一项工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该工程分成两部分,甲队做其中一部分工程用了x天,乙队做另一部分工程用了y天,若x; y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,那么两队实际各做了多少天?
-
科目: 来源: 题型:
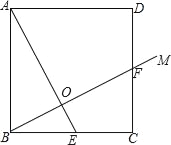
查看答案和解析>>【题目】已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.
(1)若BF⊥AE,
①求证:BF=AE;
②连接OD,确定OD与AB的数量关系,并证明;
(2)若正方形的边长为4,且BF=AE,求BO的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过建设者三年的努力,贯穿四川的“遂内高速”正式通车,已知原来从遂宁到内江的公路长150km,高速公路路程比公路缩短30km,一辆小车从遂宁到内江走高速公路的平均速度可以提高到原来的1.5倍,用时比原来减少1小时,求小车原来的平均速度和走高速的平均速度.
-
科目: 来源: 题型:
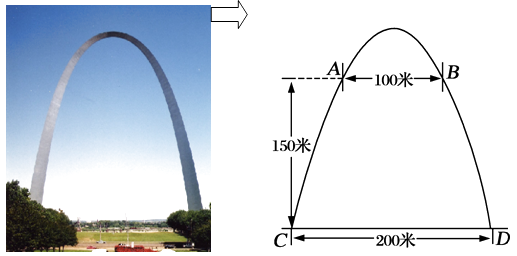
查看答案和解析>>【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.
相关试题

