【题目】密苏里州圣路易斯拱门是座雄伟壮观的抛物线形的建筑物,是美国最高的独自挺立的纪念碑,如图.拱门的地面宽度为200米,两侧距地面高150米处各有一个观光窗,两窗的水平距离为100米,求拱门的最大高度.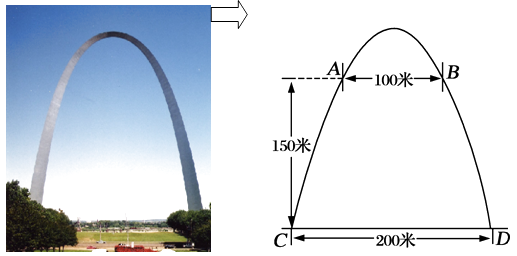
参考答案:
【答案】解:如图所示建立平面直角坐标系,此时,抛物线与x轴的交点为C(﹣100,0),D,
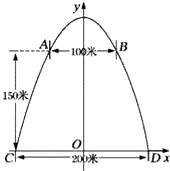
设这条抛物线的解析式为y=a(x﹣100)(x+100),
∵抛物线经过点B(50,150),可得 150=a(50﹣100)(50+100).
解得 ![]() ,∴
,∴ ![]() .
.
即得到抛物线的解析式为 ![]() ,
,
顶点坐标是(0,200)
∴拱门的最大高度为200米.
【解析】根据图形数值和抛物线与x轴的交点为C、D,抛物线经过点B,求出抛物线的解析式,顶点坐标,求出拱门的最大高度.
-
科目: 来源: 题型:
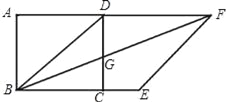
查看答案和解析>>【题目】如图,正方形ABCD中,以对角线BD为边作菱形BDFE,使B,C,E三点在同一直线上,连接BF,交CD于点G.
(1)求证:CG=CE;
(2)若正方形边长为4,求菱形BDFE的面积.
-
科目: 来源: 题型:
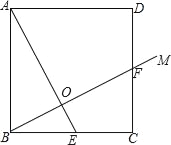
查看答案和解析>>【题目】已知:正方形ABCD,E是BC的中点,连接AE,过点B作射线BM交正方形的一边于点F,交AE于点O.
(1)若BF⊥AE,
①求证:BF=AE;
②连接OD,确定OD与AB的数量关系,并证明;
(2)若正方形的边长为4,且BF=AE,求BO的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】经过建设者三年的努力,贯穿四川的“遂内高速”正式通车,已知原来从遂宁到内江的公路长150km,高速公路路程比公路缩短30km,一辆小车从遂宁到内江走高速公路的平均速度可以提高到原来的1.5倍,用时比原来减少1小时,求小车原来的平均速度和走高速的平均速度.
-
科目: 来源: 题型:
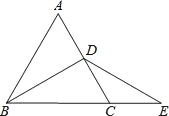
查看答案和解析>>【题目】如图,△ABC是等边三角形,BD平分∠ABC,延长BC到E,使得CE=CD.
求证:BD=DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了创建全国卫生城市,某社区要清理一个卫生死角内的垃圾,租用甲、乙两车运送,两车各运12趟可完成,需支付运费4800元.已知甲、乙两车单独运完此堆垃圾,乙车所运趟数是甲车的2倍,且乙车每趟运费比甲车少200元.
(1)求甲、乙两车单独运完此堆垃圾各需运多少趟?
(2)若单独租用一台车,租用哪台车合算?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线y=x2+bx+c经过点(2,-3)和(4,5).
(1)求抛物线的表达式及顶点坐标;
(2)将抛物线沿x轴翻折,得到图象G,求图象G的表达式;
(3)在(2)的条件下,当-2<x<2时,直线y=m与该图象有一个公共点,求m的值或取值范围.
相关试题

