【题目】已知:如图,D是BC上一点,△ABC∽△ADE,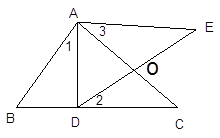
求证:∠1=∠2=∠3 .
参考答案:
【答案】证明:∵△ABC∽△ADE,
∴∠BAC=∠DAE,∠C=∠E,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠1=∠3,
又∵∠C=∠E,∠DOC=∠AOE,
∴△DOC∽△AOE,
∴∠2=∠3 ,
∴∠1=∠2=∠3
【解析】由△ABC∽△ADE,得到对应角相等,得到△DOC∽△AOE,得到∠1=∠2=∠3.
【考点精析】掌握相似三角形的判定与性质是解答本题的根本,需要知道相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图△ABC中,分别延长边AB,BC,CA,使得BD=AB,CE=2BC,AF=3CA,若△ABC的面积为1,则△DEF的面积为( )

A. 12B. 14C. 16D. 18
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AM∥BN,∠A=60°,点P是射线M上一动点(与点A不重合),BC,BD分别平分∠ABP和∠PBN,分别交射线AM于点C,D.
(1)∠CBD=
(2)当点P运动到某处时,∠ACB=∠ABD,则此时∠ABC=
(3)在点P运动的过程中,∠APB与∠ADB的比值是否随之变化?若不变,请求出这个比值:若变化,请找出变化规律.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学骑自行车去郊外春游,骑行1小时后,自行车出现故障,维修好后继续骑行,下图表示他离家的距离y(千米)与所用的时间x(时)之间关系的图象.
(1)根据图象回答:小明到达离家最远的地方用了多长时间?此时离家多远?
(2)求小明出发2.5小时后离家多远;
(3)求小明出发多长时间离家12千米.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A,B两座城市相距100千米,现计划在两城市间修筑一条高速公路(即线段AB).经测量,森林保护区中心P点既在A城市的北偏东30°的方向上,又在B城市的南偏东45°的方向上.已知森林保护区的范围是以P为圆心,35千米为半径的圆形区域内.请问:计划修筑的这条高速公路会不会穿越森林保护区?请通过计算说明.(参考数据:
 ≈1.732,
≈1.732,  ≈1.414)
≈1.414)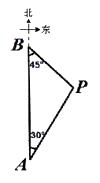
-
科目: 来源: 题型:
查看答案和解析>>【题目】一项工程,甲队单独做需40天完成,若乙队先做30天后,甲、乙两队一起合做20天恰好完成任务,请问:
(1)乙队单独做需要多少天才能完成任务?
(2)现将该工程分成两部分,甲队做其中一部分工程用了x天,乙队做另一部分工程用了y天,若x; y都是正整数,且甲队做的时间不到15天,乙队做的时间不到70天,那么两队实际各做了多少天?
-
科目: 来源: 题型:
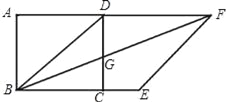
查看答案和解析>>【题目】如图,正方形ABCD中,以对角线BD为边作菱形BDFE,使B,C,E三点在同一直线上,连接BF,交CD于点G.
(1)求证:CG=CE;
(2)若正方形边长为4,求菱形BDFE的面积.
相关试题

