【题目】已知![]() 是等边三角形,
是等边三角形,![]() .
.
![]() 如图1,点E为BC上一点,点F为AC上一点,且
如图1,点E为BC上一点,点F为AC上一点,且![]() ,连接AE,BF交于点G,求
,连接AE,BF交于点G,求![]() 的度数;
的度数;
![]() 如图2,点M是BC延长线上一点,
如图2,点M是BC延长线上一点,![]() ,MN交
,MN交![]() 的外角平分线于点N,求
的外角平分线于点N,求![]() 的值;
的值;
![]() 如图3,过点A作
如图3,过点A作![]() 于点D,点P是直线AD上一点,以CP为边,在CP的下方作等边
于点D,点P是直线AD上一点,以CP为边,在CP的下方作等边![]() ,连DQ,则DQ的最小值是______.
,连DQ,则DQ的最小值是______.

参考答案:
【答案】(1)60°;(2)6;(3)1.5.
【解析】
![]() 根据等边三角形的性质得到
根据等边三角形的性质得到![]() ,
,![]() ,证明
,证明![]() ≌
≌![]() ,根据全等三角形的性质,三角形的外角的性质计算,得到答案;
,根据全等三角形的性质,三角形的外角的性质计算,得到答案;![]() 作
作![]() 交CN于H,证明
交CN于H,证明![]() ≌
≌![]() ,根据全等三角形的性质得到
,根据全等三角形的性质得到![]() ,结合图形计算即可;
,结合图形计算即可;![]() 连接BQ,证明
连接BQ,证明![]() ≌
≌![]() ,得到
,得到![]() ,根据直角三角形的性质,垂线段最短解答即可.
,根据直角三角形的性质,垂线段最短解答即可.
![]() 为等边三角形,
为等边三角形,
![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
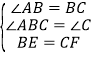 ,
,
![]() ≌
≌![]()
![]() ,
,
![]() ,
,
![]() ;
;
![]() 如图2,作
如图2,作![]() 交CN于H,
交CN于H,
![]() ,
,
![]() 是
是![]() 的外角平分线,
的外角平分线,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
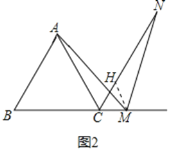
在![]() 和
和![]() 中,
中,
 ,
,
![]() ≌
≌![]()
![]() ,
,
![]() ;
;
![]() 连接BQ,
连接BQ,
![]() 是等边三角形,
是等边三角形,![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() 是等边三角形,
是等边三角形,
![]() ,
,![]() ,
,![]() ,
,
在![]() 和
和![]() 中,
中,
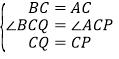 ,
,
![]() ≌
≌![]()
![]() ,
,
当![]() 时,DQ最小,最小值为
时,DQ最小,最小值为![]() ,
,
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,已知AD∥BC,AB⊥BC,点E,F在边AB上,且∠AED=45°,∠BFC=60°,AE=2,EF=2﹣
 ,FC=2
,FC=2  .
.
(1)BC= ;
(2)求点D到BC的距离;
(3)求DC的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:若
 ,求m,n的值.
,求m,n的值.解:
 ,
, .
. ,
, ,
, ,
, ,
, ,
, ,
,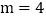 .
.根据你的观察,探究下面的问题:
(1)已知:
 ,求
,求 的值;
的值;(2)已知:
 的三边长a,b,c都是正整数,且满足:
的三边长a,b,c都是正整数,且满足: ,求
,求 的最大边c的值;
的最大边c的值;(3)已知:
 ,
, ,直接写出a的值.
,直接写出a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下图是某同学在沙滩上用石于摆成的小房子.

观察图形的变化规律,写出第n个小房子用了___________________块石子.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算
(1)-2a2(
 ab+b2)-5a(a2b-ab2)
ab+b2)-5a(a2b-ab2)(2)计算9(x+2)(x-2)-(3x-2)2
(3)计算(a-b+c)(a-b-c)
(4)用乘法公式计算:
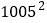
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班要从甲、乙两名同学中选拔出一人,代表班级参加学校的一分钟踢毽子体能素质比赛,在一段时间内的相同条件下,甲、乙两人进行了六场一分钟踢毽子的选拔测试,根据他们的成绩绘制出如图的统计表和不完整的折线统计图.
甲、乙两人选拔测试成绩统计表甲成绩
(次/min)乙成绩
(次/min)第1场
87
87
第2场
94
98
第3场
91
87
第4场
85
89
第5场
91
100
第6场
92
85
中位数
91
n
平均数
m
91
并计算出乙同学六场选拔测试成绩的方差:
S乙2=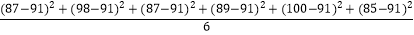 =
= 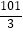
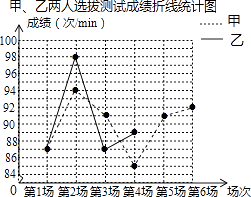
(1)m= , n= , 并补全全图中甲、乙两人选拔测试成绩折线统计图;
(2)求甲同学六场选拔测试成绩的方差S甲2;
(3)分别从平均数、中位数和方差的角度分析比较甲、乙二人的成绩各有什么特点?
(4)经查阅该校以往本项比赛的资料可知,①成绩若达到90次/min,就有可能夺得冠军,你认为选谁参赛更有把握夺冠?为什么?
②该项成绩的最好记录是95次/min,就有可能夺得冠军,你认为选谁参赛更有把握夺冠?为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点P在第一象限角平分线上,点A在x轴的正半轴运动,点B在y轴上,且
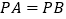 .
.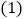 如图1,点B在y轴的正半轴上,
如图1,点B在y轴的正半轴上,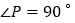 ,
,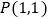 ,则
,则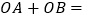 ______;
______;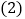 如图2,点B与原点重合,
如图2,点B与原点重合,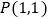 ,点Q是OP延长线上一点,连接QA,过点P作
,点Q是OP延长线上一点,连接QA,过点P作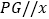 轴,与QA相交于点G,过点P作x轴的垂线,垂足是点H,过点A作QA的垂线与PH相交于点E,过点E作
轴,与QA相交于点G,过点P作x轴的垂线,垂足是点H,过点A作QA的垂线与PH相交于点E,过点E作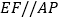 ,与x轴相交于点F,若
,与x轴相交于点F,若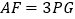 ,求点E的坐标;
,求点E的坐标;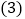 如图3,点B在y轴的负半轴上,PB与x轴相交于点D,连接AB,AO平分
如图3,点B在y轴的负半轴上,PB与x轴相交于点D,连接AB,AO平分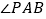 ,过点P作
,过点P作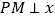 轴于点M,求
轴于点M,求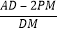 的值.
的值.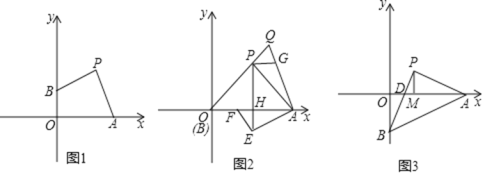
相关试题

