【题目】如图,在四边形ABCD中,已知AD∥BC,AB⊥BC,点E,F在边AB上,且∠AED=45°,∠BFC=60°,AE=2,EF=2﹣ ![]() ,FC=2
,FC=2 ![]() .
.
(1)BC= ;
(2)求点D到BC的距离;
(3)求DC的长.
参考答案:
【答案】
(1)3
(2)解:过点D作DG⊥BC于点G,
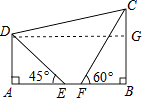
∵AD∥BC,AB⊥BC,
∴DG=AB,DA⊥AB,
∵FC=2 ![]() ,∠BFC=60°,
,∠BFC=60°,
∴BF=FCcos60°= ![]() ,
,
∴DG=AB=AE+EF+BF=2+2﹣ ![]() +
+ ![]() =4
=4
(3)解:∵DA⊥AB,∠AED=45°,
∴AD=AE=2,
∵DG⊥BC,AB⊥BC,
∴DG∥AB,
∵AD∥BC,
∴四边形ABGD是矩形,
∴BG=AD=2,
∴CG=BC﹣BG=3﹣2=1,
∴在Rt△DCG中,CD= ![]() =
= ![]()
【解析】解:(1)∵AB⊥BC,
∴∠B=90°,
∵FC=2 ![]() ,∠BFC=60°,
,∠BFC=60°,
∴BC=FCsin60°=2 ![]() ×
× ![]() =3;
=3;
所以答案是:3.
【考点精析】关于本题考查的勾股定理的概念和解直角三角形,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,爸爸从家(点O)出发,沿着等腰三角形AOB的边OA→AB→BO的路径去匀速散步,其中OA=OB.设爸爸距家(点O)的距离为S,散步的时间为t,则下列图形中能大致刻画S与t之间函数关系的图象是( )

A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)先化简,再求值: ÷(1+
÷(1+  ),其中x=2017.
),其中x=2017.
(2)已知方程x2﹣2x+m﹣3=0有两个相等的实数根,求m的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某村为了尽早摆脱贫穷落后的现状,积极响应国家号召,15位村民集资8万元,承包了一些土地种植有机蔬菜和水果,种这两种作物每公顷需要人数和投入资金如下表:
作物种类
每公顷所需人数/人
每公顷投入资金/万元
蔬菜
4
2
水果
5
3
在现有条件下,这15位村民应承包多少公顷土地,怎样安排能使每人都有事可做,并且资金正好够用?
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读材料:若
 ,求m,n的值.
,求m,n的值.解:
 ,
, .
. ,
, ,
, ,
, ,
, ,
, ,
, .
.根据你的观察,探究下面的问题:
(1)已知:
 ,求
,求 的值;
的值;(2)已知:
 的三边长a,b,c都是正整数,且满足:
的三边长a,b,c都是正整数,且满足: ,求
,求 的最大边c的值;
的最大边c的值;(3)已知:
 ,
, ,直接写出a的值.
,直接写出a的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】下图是某同学在沙滩上用石于摆成的小房子.

观察图形的变化规律,写出第n个小房子用了___________________块石子.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知
 是等边三角形,
是等边三角形, .
. 如图1,点E为BC上一点,点F为AC上一点,且
如图1,点E为BC上一点,点F为AC上一点,且 ,连接AE,BF交于点G,求
,连接AE,BF交于点G,求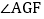 的度数;
的度数; 如图2,点M是BC延长线上一点,
如图2,点M是BC延长线上一点, ,MN交
,MN交 的外角平分线于点N,求
的外角平分线于点N,求 的值;
的值; 如图3,过点A作
如图3,过点A作 于点D,点P是直线AD上一点,以CP为边,在CP的下方作等边
于点D,点P是直线AD上一点,以CP为边,在CP的下方作等边 ,连DQ,则DQ的最小值是______.
,连DQ,则DQ的最小值是______.
相关试题

