【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度,平面直角坐标系xOy的原点O在格点上,x轴、y轴都在网格线上,△ABC的顶点A、B、C都在格点上.
(1)将△ABC向左平移两个单位得到△A1B1C1,请在图中画出△A1B1C1.
(2)△ABC和△A2B2C2关于原点O成中心对称,请在图中画出△A2B2C2.
(3)请写出C2的坐标 ,并判断以点B1、C1、B2、C2为顶点的四边形是 .

参考答案:
【答案】(1)见解析(2)见解析(3)(3,1);矩形
【解析】
(1)分别画出A、B、C的对应点A1、B1、C1 即可;
(2)分别画出A、B、C的对应点A2、B2、C2即可;
(3)观察图象即可求得C2的坐标,然后利用勾股定理求得四边形边长及对角线长度,从而解决问题.
(1)△A1B1C1如图所示;
(2)△A2B2C2如图所示;
(3)由图可知C2(3,1),
∵B1C1=![]() ,B2C2=
,B2C2=![]() ,∴B1C1= B2C2
,∴B1C1= B2C2
∵B1C2=![]() ,B2C1=
,B2C1=![]() ,∴B1C2= B2C1
,∴B1C2= B2C1
∴四边形B1C1B2C2为平行四边形,
∵B1B2=![]() ,C2C1=
,C2C1=![]() ,∴B1B2= C2C1
,∴B1B2= C2C1
∴平行四边形B1C1B2C2为矩形,
故答案为:(3,1);矩形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某球迷协会组织36名球迷拟租乘汽车赴比赛场地,为首次打进世界杯决赛圈的国家足球队加油助威.可租用的汽车有两种:一种每辆可乘8人,另一种每辆可乘4人,要求租用的车子不留空座,也不超载.
(1)请你给出不同的租车方案(至少三种);
(2)若8个座位的车子的租金是300元/天,4个座位的车子的租金是200元/天,请你设计出费用最少的租车方案,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,BE平分∠ABC,交AD于点E、F是BC上一点,且CF=AE,连接DF.
(1)求证:四边形BEDF是平行四边形;
(2)若∠ABC=70°,求∠CDF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知
 ,
, ,其中
,其中 ,
, 满足
满足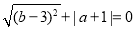 ,点
,点 为第三象限内一点.
为第三象限内一点.
(1)若
 到坐标轴的距离相等,
到坐标轴的距离相等, ,且
,且 ,求
,求 点坐标
点坐标(2)若
 为
为 ,请用含
,请用含 的式子表示
的式子表示 的面积.
的面积.(3)在(2)条件下,当
 时,在
时,在 轴上有点
轴上有点 ,使得
,使得 的面积是
的面积是 的面积的2倍,请求出点
的面积的2倍,请求出点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】改革开放以来,我国国民经济保持良好发展势头,国内生产总值持续较快增长, 下图是1998年~2002年国内生产总值统计图.

(1)从图中可看出1999年国内生产总值是___________.
(2)已知2002年国内生产总值比2000年增加12956亿元,2001年比2000年增加6491亿元,求2002年国内生产总值比2001年增长的百分率(结果保留两个有效数字).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1和2,在20×20的等距网格(每格的宽和高均是1个单位长)中,Rt△ABC从点A与点M重合的位置开始,以每秒1个单位长的速度先向下平移,当BC边与网的底部重合时,继续同样的速度向右平移,当点C与点P重合时,Rt△ABC停止移动.设运动时间为x秒,△QAC的面积为y.
(1)如图1,当Rt△ABC向下平移到Rt△A1B1C1的位置时,请你在网格中画出Rt△A1B1C1关于直线QN成轴对称的图形;
(2)如图2,在Rt△ABC向下平移的过程中,请你求出y与x的函数关系式,并说明当x分别取何值时,y取得最大值和最小值?最大值和最小值分别是多少?
(3)在Rt△ABC向右平移的过程中,请你说明当x取何值时,y取得最大值和最小值?最大值和最值分别是多少?为什么?(说明:在(3)中,将视你解答方法的创新程度,给予1~4分的加分)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知Rt△ABC中,AC=5,BC=12,∠ACB=90°,P是AB边上的动点(与点A、B不重合),Q是BC边上的动点(与点B、C不重合)
(1)如图,当PQ∥AC,且Q为BC的中点时,求线段CP的长;
(2)当PQ与AC不平行时,△CPQ可能为直角三角形吗?若有可能,请求出线段CQ的长的取值范围;若不可能,请说明理由.

相关试题

