【题目】某球迷协会组织36名球迷拟租乘汽车赴比赛场地,为首次打进世界杯决赛圈的国家足球队加油助威.可租用的汽车有两种:一种每辆可乘8人,另一种每辆可乘4人,要求租用的车子不留空座,也不超载.
(1)请你给出不同的租车方案(至少三种);
(2)若8个座位的车子的租金是300元/天,4个座位的车子的租金是200元/天,请你设计出费用最少的租车方案,并说明理由.
参考答案:
【答案】(1)详见解析;(2)最佳方案为四辆8人车,一辆4人车.
【解析】试题分析:
(1)设载客8人的车租x辆,载客4人的车租y辆,由题意可得:8x+4y=36,找出该方程的自然数解即可得到答案;
(2)设总的租车费用为w,则结合(1)可得:w=300x+200y,由8x+4y=36可得:y=-2x+9,由此可得w=-100x+1800;由![]() 可得
可得![]() ;结合一次函数的性质即可得到当x=4时,w最小,从而可得总费用最少的租车方案.
;结合一次函数的性质即可得到当x=4时,w最小,从而可得总费用最少的租车方案.
试题解析:
(1)设载客8人的车租x辆,载客4人的车租y辆,由题意可得:
8x+4y=36,
∵该方程的自然数解有: ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
∴共有如下5种租车方案:
方案1:四辆8人车,一辆4人车4×8+1×4=36.
方案2:三辆8人车,三辆4人车3×8+3×4=36.
方案3:二辆8人车,五辆4人车2×8+5×4=36.
方案4:一辆8人车,七辆4人车1×8+7×4=36.
方案5:九辆4人车9×4=36.
(2)设8座车x辆,4座车y辆,总费用为w,则:w=300x+200y.
∵8x+4y=36,
∴y=-2x+9,
∴w=1800﹣100x.
∴w随x的增大而减小,
∵0≤8x≤36,
∴0≤x≤4.5,
又因为x只能取整数,
∴当x取最大整数值,即x=4时,w的值最小.
答:最佳方案为租四辆8人车,一辆4人车.
-
科目: 来源: 题型:
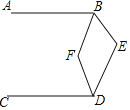
查看答案和解析>>【题目】如图,
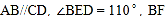 平分
平分 平分
平分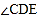 ,则
,则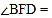 ______ .
______ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2+2x﹣3,
(1)用描点法画出y=x2+2x﹣3的图象.
(2)根据你所画的图象回答问题:当x 时,函数值y随x的增大而增大,当x 时,函数值y随x的增大而减小.
解:列表得:
X
Y
描点、连线

-
科目: 来源: 题型:
查看答案和解析>>【题目】在一块长16m,宽12m的矩形荒地上建造一个花园,要求花轩占地面积为荒地面积的一半,下面分别是小强和小颖的设计方案.
(1)你认为小强的结果对吗?请说明理由.

(2)请你帮助小颖求出图中的x.
(3)你还有其他的设计方案吗?请在图(3)中画出一个与图(1)(2)有共同特点的设计草图,并加以说明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在ABCD中,BE平分∠ABC,交AD于点E、F是BC上一点,且CF=AE,连接DF.
(1)求证:四边形BEDF是平行四边形;
(2)若∠ABC=70°,求∠CDF的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知
 ,
, ,其中
,其中 ,
, 满足
满足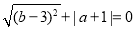 ,点
,点 为第三象限内一点.
为第三象限内一点.
(1)若
 到坐标轴的距离相等,
到坐标轴的距离相等, ,且
,且 ,求
,求 点坐标
点坐标(2)若
 为
为 ,请用含
,请用含 的式子表示
的式子表示 的面积.
的面积.(3)在(2)条件下,当
 时,在
时,在 轴上有点
轴上有点 ,使得
,使得 的面积是
的面积是 的面积的2倍,请求出点
的面积的2倍,请求出点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度,平面直角坐标系xOy的原点O在格点上,x轴、y轴都在网格线上,△ABC的顶点A、B、C都在格点上.
(1)将△ABC向左平移两个单位得到△A1B1C1,请在图中画出△A1B1C1.
(2)△ABC和△A2B2C2关于原点O成中心对称,请在图中画出△A2B2C2.
(3)请写出C2的坐标 ,并判断以点B1、C1、B2、C2为顶点的四边形是 .

相关试题

