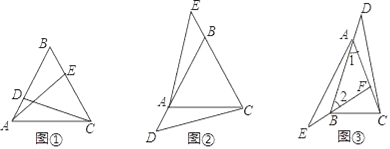
【题目】【感知】如图①,△ABC是等边三角形,点D、E分别在AB、BC边上,且AD=BE,易知:△ADC≌△BEA.
【探究】如图②,△ABC是等边三角形,点D、E分别在边BA、CB的延长线上,且AD=BE,△ADC与△BEA还全等吗?如果全等,请证明:如果不全等,请说明理由.
【拓展】如图③,在△ABC中,AB=AC,∠1=∠2,点D、E分别在BA、FB的延长线上,且AD=BE,若AF=![]() CF=2BE,S△ABF=6,则S△BCD的大小为 .
CF=2BE,S△ABF=6,则S△BCD的大小为 .
参考答案:
【答案】探究:△ADC与△BEA全等,理由见解析;拓展:S△BCD=13
【解析】试题分析:探究:利用平角的定义得出∠DAC=∠EBA即可得出结论;
拓展:先判断出△ADC≌△BEA,进而得出S△ADC=S△BEA,再利用同高的两三角形的面积的比等于底的比求出△ABE,△BCF的面积,即可得出结论.
试题解析:探究:△ADC与△BEA全等,
理由:在等边三角形ABC中,AB=AC,∠BAC=∠ABC=60°,
∴∠DAC=180°﹣∠BAC=120°,∠EBA=180°﹣∠ABC=120°,
∴∠DAC=∠EBA,
∵AD=BE,
∴△ADC≌△BEA;
拓展:∵∠1=∠2,
∴AF=BF,∠DAC=∠EBA,
∵AD=BE,AC=AB,
∴△ADC≌△BEA(SAS),
∴S△ADC=S△BEA,
∵AF=2BE,AF=BF,
∴BF=2BE,
∴S△ABE=![]() S△ABF=3(同高的两三角形的面积比是底的比),
S△ABF=3(同高的两三角形的面积比是底的比),
∴S△ADC=3,
∵AF=![]() CF,
CF,
∴S△BFC=![]() S△ABF=4(同高的两三角形的面积比是底的比),
S△ABF=4(同高的两三角形的面积比是底的比),
∴S△BCD=S△BCF+S△ABF+S△ADC=13,
故答案为13.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(x+m)(x2﹣3x+n)的积中不含x2、x项,求m和n的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】运动会上裁判员测量跳远成绩时,先在距离踏板最近的跳远落地点上插上作为标记的小旗,再以小旗的位置为赤字的零点,将尺子拉直,并与踏板边缘所在直线垂直,把尺子上垂足点表示的数作为跳远成绩.这实质上是数学知识____________在生活中的应用.
-
科目: 来源: 题型:
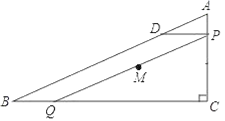
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P从点A出发沿边AC向点C以每秒1个单位长度的速度运动,同时点Q从点C出发沿边CB向点B以每秒a个单位长度的速度运动,过点P作PD⊥BC,交AB于点D,连接PQ.当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)当a=2时,解答下列问题:
①QB= ,PD= .(用含t的代数式分别表示)
②通过计算说明,不存在t的值使得四边形PDBQ为菱形.
(2)当a为某个数值时,四边形PDBQ在某一时刻为菱形,求a的值及四边形PDBQ为菱形时t的值.
(3)当t=2时,在整个运动过程中,恰好存在线段PQ的中点M到△ABC三边距离相等,直接写出此刻a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某初级中学附近路口的汽车流量,交通管理部门调查了某周一至周五下午放学时间段通过该路口的汽车数量(单位:辆),结果如下: 183 191 169 190 177
则在该时间段中,通过这个路口的汽车数量的平均数是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】数学李老师给学生出了这样一个问题:探究函数y=
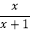 图象与性质.小斌根据学习函数的经验,对函数y=
图象与性质.小斌根据学习函数的经验,对函数y=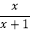 的图象与性质进行了探究.下面是小斌的探究过程,请补充完成:
的图象与性质进行了探究.下面是小斌的探究过程,请补充完成:(1)函数y=
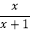 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;(2)根据下表所列出y与x对应值,在平面直角坐标系中描出各对以对应值为坐标的点,并画出该函数的图象;

(3)若直线y=x+b与函数y=
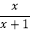 的图象无交点,请直接写出b的取值范围.
的图象无交点,请直接写出b的取值范围. 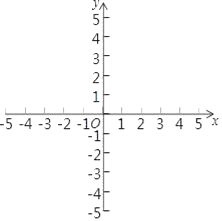
-
科目: 来源: 题型:
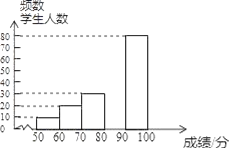
查看答案和解析>>【题目】为了传承优秀传统文化,某校团委组织了一次全校3000名学生参加的“汉字听写”大赛,赛后发现所有参赛学生的成绩均不低于50分.为了更好的了解本次大赛的成绩分布情况,随机抽取了其中200名学生的成绩,(成绩x取整数,总分100分)作为样本进行整理,得到下列不完整的统计图表:
成绩/分
频数
频率
50≤x<60
10
0.05
60≤x<70
20
0.10
70≤x<80
30
b
80≤x<90
a
0.30
90≤x≤100
80
0.40
请根据所给信息,解答下列问题:
(1)a= ,b= ;
(2)请补全频数分布直方图;
(3)若成绩在90分以上(包括90分)的为“优”等,则该校参加这次比赛的3000名学生中成绩“优”等的人数.
相关试题

