【题目】若(x+m)(x2﹣3x+n)的积中不含x2、x项,求m和n的值.
参考答案:
【答案】解:原式=x3﹣3x2+nx+mx2﹣3mx+mn=x3+(m﹣3)x2+(n﹣3m)x+mn,
由题意得到m﹣3=0,n﹣3m=0,
解得:m=3,n=9.
【解析】原式利用多项式乘以多项式法则计算得到结果,由题意得到x2、x项系数为0,求出m与n的值即可.
【考点精析】通过灵活运用多项式乘多项式,掌握多项式与多项式相乘,先用一个多项式的每一项乘另外一个多项式的每一项,再把所得的积相加即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组线段中,能组成三角形的是( )
A. 1cm,2cm,3cm B. 2cm,3cm,4cm
C. 1cm,8cm,4cm D. 4cm,4cm,8cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( )
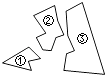
A.带①去
B.带②去
C.带③去
D.带①和②去 -
科目: 来源: 题型:
查看答案和解析>>【题目】关于整式(x﹣2)(x+n)运算结果中,一次项系数为2,则n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】运动会上裁判员测量跳远成绩时,先在距离踏板最近的跳远落地点上插上作为标记的小旗,再以小旗的位置为赤字的零点,将尺子拉直,并与踏板边缘所在直线垂直,把尺子上垂足点表示的数作为跳远成绩.这实质上是数学知识____________在生活中的应用.
-
科目: 来源: 题型:
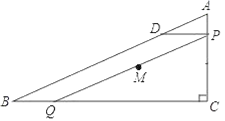
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,点P从点A出发沿边AC向点C以每秒1个单位长度的速度运动,同时点Q从点C出发沿边CB向点B以每秒a个单位长度的速度运动,过点P作PD⊥BC,交AB于点D,连接PQ.当其中一点到达端点时,另一点也随之停止运动,设运动时间为t秒(t≥0).
(1)当a=2时,解答下列问题:
①QB= ,PD= .(用含t的代数式分别表示)
②通过计算说明,不存在t的值使得四边形PDBQ为菱形.
(2)当a为某个数值时,四边形PDBQ在某一时刻为菱形,求a的值及四边形PDBQ为菱形时t的值.
(3)当t=2时,在整个运动过程中,恰好存在线段PQ的中点M到△ABC三边距离相等,直接写出此刻a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【感知】如图①,△ABC是等边三角形,点D、E分别在AB、BC边上,且AD=BE,易知:△ADC≌△BEA.
【探究】如图②,△ABC是等边三角形,点D、E分别在边BA、CB的延长线上,且AD=BE,△ADC与△BEA还全等吗?如果全等,请证明:如果不全等,请说明理由.
【拓展】如图③,在△ABC中,AB=AC,∠1=∠2,点D、E分别在BA、FB的延长线上,且AD=BE,若AF=
 CF=2BE,S△ABF=6,则S△BCD的大小为 .
CF=2BE,S△ABF=6,则S△BCD的大小为 .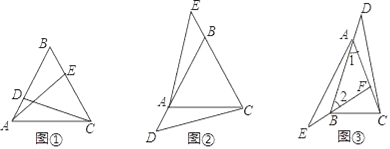
相关试题

