【题目】如图,在Rt△ABC中,∠ACB=90°,以BC为半径作⊙B,交AB于点D,交AB的延长线于点E,连接CD、CE. 
(1)求证:△ACD∽△AEC;
(2)当 ![]() =
= ![]() 时,求tanE;
时,求tanE;
(3)若AD=4,AC=4 ![]() ,求△ACE的面积.
,求△ACE的面积.
参考答案:
【答案】
(1)证明:∵DE为直径,
∴∠DCE=90°,即∠2+∠DCB=90°,
∵∠ACB=90°,即∠1+∠DCB=90°,
∴∠1=∠2,
而∠CAD=∠EAC,
∴△ACD∽△AEC
(2)解:由 ![]() =
= ![]() ,设AC=4k,则BC=3k,
,设AC=4k,则BC=3k,
∴BD=BE=3k,
∴AB= ![]() =5k,
=5k,
∴AE=AB+BE=5k+3k=8k,
在Rt△CDE中,tanE= ![]() ,
,
∵△ACD∽△AEC,
∴ ![]() =
= ![]() =
= ![]() =
= ![]() ,
,
∴tanE= ![]()
(3)作CH⊥AE于H,如图,
∵△ACD∽△AEC,
∴ ![]() =
= ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,解得AE=12,CE=
,解得AE=12,CE= ![]() CD,
CD,
∴DE=AE﹣AC=8,
在Rt△CDE中,∵tanE= ![]() =
= ![]() =
= ![]() ,
,
∴∠E=30°,
∴CD= ![]() DE=4,CE=4
DE=4,CE=4 ![]() ,
,
在Rt△CHE中,CH= ![]() CE=2
CE=2 ![]() ,
,
∴△ACE的面积= ![]() ×12×2
×12×2 ![]() =12
=12 ![]() .
.

【解析】(1)利用圆周角定理得到∠DCE=90°,而∠ACB=90°,则∠1=∠2,加上公共角,则可判断△ACD∽△AEC;(2)利用由 ![]() =
= ![]() 设AC=4k,BC=3k,由勾股定理计算出AB=5k,则AE=8k,再由△ACD∽△AEC,利用相似比得到
设AC=4k,BC=3k,由勾股定理计算出AB=5k,则AE=8k,再由△ACD∽△AEC,利用相似比得到 ![]() =
= ![]() =
= ![]() ,然后根据正切的定义可得tanE的值;(3)作CH⊥AE于H,如图,由△ACD∽△AEC,利用相似比得到AE=12,CE=
,然后根据正切的定义可得tanE的值;(3)作CH⊥AE于H,如图,由△ACD∽△AEC,利用相似比得到AE=12,CE= ![]() CD,则DE=AE﹣AC=8,在Rt△CDE中利用三角函数和特殊角的三角形函数值得到∠E=30°,则可计算出CD=
CD,则DE=AE﹣AC=8,在Rt△CDE中利用三角函数和特殊角的三角形函数值得到∠E=30°,则可计算出CD= ![]() DE=4,CE=4
DE=4,CE=4 ![]() ,接着计算出CH,然后根据三角形面积公式求解.
,接着计算出CH,然后根据三角形面积公式求解.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=x2﹣(2m+1)+(
 m2﹣1).
m2﹣1).
(1)求证:不论m取什么实数,该二次函数图象与x轴总有两个交点;
(2)若该二次函数图象经过点(2m﹣2,﹣2m﹣1),求该二次函数的表达式. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,AC、BD相交于点F,点E在BD上,且
 .
. 
(1)试问:∠BAE与∠CAD相等吗?为什么?
(2)试判断△ABE与△ACD是否相似?并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,操场上有一根旗杆AH,为测量它的高度,在B和D处各立一根高1.5米的标杆BC、DE,两杆相距30米,测得视线AC与地面的交点为F,视线AE与地面的交点为G,并且H、B、F、D、G都在同一直线上,测得BF为3米,DG为5米,求旗杆AH的高度?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,试求∠DFB和∠DGB的度数.

-
科目: 来源: 题型:
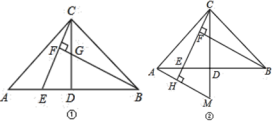
查看答案和解析>>【题目】已知:在△ABC中,AC=BC,∠ACB=90°,点D是AB的中点,点E是AB边上一点.
(1)直线BF垂直直线CE于点F,交CD于点G(如图①),求证:AE=CG;
(2)直线AH垂直于直线CE,垂足为点H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为了提升初中学生学习数学的兴趣,培养学生的创新精神,举办“玩转数学”比赛.现有甲、乙两个小组进入决赛,评委从研究报告、小组展示、答辩三个方面为各小组打分,各项成绩均按百分制记录.甲、乙两个小组各项得分如下表:
小组
研究报告
小组展示
答辩
甲
91
80
78
乙
79
83
90
(1)计算各小组的平均成绩,并从高分到低分确定小组的排名顺序;
(2)如果研究报告、小组展示、答辩按照4:3:3计算成绩,哪个小组的成绩最高?
相关试题

