Question

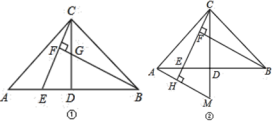
【题目】已知：在△ABC中，AC=BC，∠ACB=90°，点D是AB的中点，点E是AB边上一点．

（1）直线BF垂直直线CE于点F，交CD于点G（如图①），求证：AE=CG；

（2）直线AH垂直于直线CE，垂足为点H，交CD的延长线于点M（如图②），找出图中与BE相等的线段，并证明．

Answer 1

【答案】(1)见解析;(2)见解析.

【解析】

（1）首先根据点D是AB中点，∠ACB=90°，可得出∠ACD=∠BCD=45°，判断出△AEC≌△CGB，即可得出AE=CG；
（2）根据垂直的定义得出∠CMA+∠MCH=90°，∠BEC+∠MCH=90°，再根据AC=BC，∠ACM=∠CBE=45°，得出△BCE≌△CAM，进而证明出BE=CM．

(1)证明：因为直线垂直

所以∠CFB=90°，所以∠ECB+∠CBF=90°.

又因为，所以

因为点是的中点，所以

又所以≌，

所以.

因为，所以.

因为∠ACE=∠CBF，∠DCB=∠A，AC=BC，所以△CAE≌△BCG，所以AE=CG.

≌

.

(2)解：BE=CM.证明： 因为 ∠ACB=90°,所以 ∠ACH +∠BCF=90°.

因为 CH⊥AM，即∠CHA=90°,所以 ∠ACH +∠CAH=90°,所以 ∠BCF=∠CAH.

在△BCE与△CAM中,BC=CA ,∠BCF=∠CAH,

由（1）知∠CBE=∠ACM,

所以△BCE≌△CAM.所以BE=CF.