【题目】如图,在正方形ABCD内有一点P满足AP=AB,PB=PC,连接AC、PD. 
求证:
(1)△APB≌△DPC;
(2)∠BAP=2∠PAC.
参考答案:
【答案】
(1))解:∵四边形ABCD是正方形,∴∠ABC=∠DCB=90°.
∵PB=PC,∴∠PBC=∠PCB.
∴∠ABC﹣∠PBC=∠DCB﹣∠PCB,即∠ABP=∠DCP.
又∵AB=DC,PB=PC,
∴△APB≌△DPC.
(2))解:证明:∵四边形ABCD是正方形,
∴∠BAC=∠DAC=45°.
∵△APB≌△DPC,∴AP=DP.
又∵AP=AB=AD,∴DP=AP=AD.
∴△APD是等边三角形.
∴∠DAP=60°.
∴∠PAC=∠DAP﹣∠DAC=15°.
∴∠BAP=∠BAC﹣∠PAC=30°.
∴∠BAP=2∠PAC.
【解析】(1)AP=AB,PB=PC,∴∠ABC﹣∠PBC=∠DCB﹣∠PCB,即∠ABP=∠DCP,因此可证得两三角形全等.(2)有(1)∠CAD=45°,△PAD为等边三角形,可求得∠BAP=30°∠PAC=∠PAD﹣∠CAD=15°,因此可证的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,AC=BC=a,以斜边AB上的点O为圆心的圆分别与AC,BC相切于点E,F,与AB分别交于点G,H,且EH的延长线和CB的延长线交于点D,则CD的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD绕点A逆时针旋转30°,得到□AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),点B′恰好落在BC边上,则∠C=( )

A.155° B.170° C.105° D.145°
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)20170﹣|﹣sin45°|cos45°+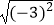 ﹣(﹣
﹣(﹣  )﹣1
)﹣1
(2) .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两校分别有一男一女共4名教师报名到农村中学支教.
(1)若从甲、乙两校报名的教师中分别随机选1名,则所选的2名教师性别相同的概率是 .
(2)若从报名的4名教师中随机选2名,用列表或画树状图的方法求出这2名教师来自同一所学校的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解“数学思想作为对学习数学帮助有多大?”一研究员随机抽取了一定数量的高校大一学生进行了问卷调查,并将调查得到的数据用下面的扇形图和下表来表示(图、表都没制作完成).
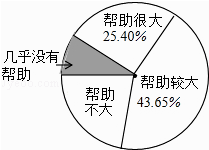
选项
帮助很大
帮助较大
帮助不大
几乎没有帮助
人数
a
543
269
b
根据图、表提供的信息.
(1)请问:这次共有多少名学生参与了问卷调查?
(2)算出表中a、b的值. (注:计算中涉及到的“人数”均精确到1) -
科目: 来源: 题型:
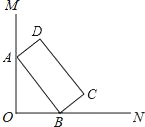
查看答案和解析>>【题目】如图,∠MON=90°,矩形ABCD的顶点A、B分别在边OM,ON上,当B在边ON上运动时,A随之在边OM上运动,矩形ABCD的形状保持不变,其中AB=2,BC=1,运动过程中,点D到点O的最大距离为( )
A.
 +1 B.
+1 B.  C.
C.  D.
D. 
相关试题

