【题目】已知抛物线y=ax2-2ax+c与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且OC=3OA.

(1)求抛物线的函数表达式;
(2)直接写出直线BC的函数表达式;
(3)如图1,D为y轴的负半轴上的一点,且OD=2,以OD为边作正方形ODEF.将正方形ODEF以每秒1个单位的速度沿x轴的正方向移动,在运动过程中,设正方形ODEF与△OBC重叠部分的面积为s,运动的时间为t秒(0<t≤2).
求:①s与t之间的函数关系式;
②在运动过程中,s是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(4)如图2,点P(1,k)在直线BC上,点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的平行四边形?若存在,请直接写出M点坐标;若不存在,请说明理由.
参考答案:
【答案】(1)y=x2-2x-3 ;
(2)直线BC的函数表达式为y=x-3;
(3)①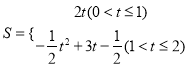
②当t =2秒时,S有最大值,最大值为![]() .
.
(4)存在符合条件的点M,且坐标为M 1(-![]() ,
,![]() ),M2(
),M2(![]() ,
,![]() ), M3(
), M3(![]() ,
,![]() ),M4(
),M4(![]() ,
,![]() )
)
【解析】分析:(1)先由OC、OA的数量关系确定点C的坐标,然后利用待定系数法可求出抛物线的解析式; (2)由(1)的抛物线解析式可得点B的坐标,结合点C的坐标,利用待定系数法求解即可; (3)①首先要明确正方形ODEF和△OBC重合部分的形状:当点D在△OBC内部时,两者的重合部分是矩形;当点D在△OBC外部时,两者的重合部分是五边形,其面积可由正方形的面积减去△ 的面积(G、H分别为 、 和线段BC的交点).在判断t的取值范围时,要注意一个“关键点”即点D位于线段BC上时; ②根据①的函数性质即可得到答案. (4)若存在以A、M、N、P为顶点的平行四边形,应分AM PN或AN PM两种情况.由于AM在x轴上,结合平行四边形的特点可知:无论哪种情况,点N到x轴的距离都等于点P到x轴的距离,根据这个特点可确定点M、N的坐标.
本题解析:(1)∵ A(-1,0), ![]() ,C(0,-3)
,C(0,-3)
∵抛物线经过A(-1,0),C(0,-3)
∴![]() ,∴
,∴![]() ,
,
∴y=x2-2x-3
(2)由(1)的抛物线解析式可知:点B(3,0).
设直线BC的解析式为y=kx+b.
将B(3,0),C(0,-3)代入得![]() ,解得
,解得![]() ,
,
∴直线BC的函数表达式为y=x-3.
(3)当正方形ODEF的顶点D运动到直线BC上时,设D点的坐标为(m,-2),
根据题意得: -2=m-3,∴m=1
①当0<t≤1时,S1=2t
当1<t≤2时
S2=![]() =2t-
=2t-![]()
=-![]() ,
,
②当t =2秒时,S有最大值,最大值为![]()
(4)由(2)知:点P(1,-2),假设存在符合条件的点M.
①当AM∥PN,AM=PN时,点N、P的纵坐标相同,
即点N的纵坐标为-2,代入抛物线的解析式中得x-2x-3=-2,
解得 x=1±![]() ,
,
∴AM=NP=![]() ,
,
∴M 1(-![]() ,0) M2(
,0) M2(![]() ,0),
,0),
②当AN∥PM,AN=PM时,平行四边形的对角线PN、AM互相平分.
设M(m,0),则N(m-2,2).
将点N的坐标代入抛物线的解析式中,得(m-2)-2(m-2)-3=2,
解得 m=3±![]() ,
,
∴M3(3-![]() ,0) M4(3+
,0) M4(3+![]() ,0 ).
,0 ).
综上,存在符合条件的M点,且坐标为:
M 1(-![]() ,0) M2(
,0) M2(![]() ,0)
,0)
M3(3-![]() ,0) M4(3+
,0) M4(3+![]() ,0 )
,0 )
-
科目: 来源: 题型:
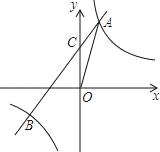
查看答案和解析>>【题目】如图,反比例函数y=
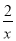 的图象与一次函数y=kx+b的图象交于点A(m,2),点B(﹣2,n ),一次函数图象与y轴的交点为C.
的图象与一次函数y=kx+b的图象交于点A(m,2),点B(﹣2,n ),一次函数图象与y轴的交点为C.(1)求一次函数解析式;
(2)求C点的坐标;
(3)求△AOB的面积.
-
科目: 来源: 题型:
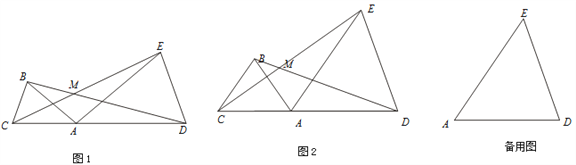
查看答案和解析>>【题目】已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段 BD、CE交于点M.
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;②求∠BMC的大小(用α表示);
(2)如图2,若AB= BC=kAC,AD =ED=kAE 则线段BD与CE的数量关系为 ,∠BMC= (用α表示);
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺规作图,不写作法,保留作图痕迹),连接 EC并延长交BD于点M.则∠BMC= (用α表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4…
利用你的发现的规律解决下列问题
(1)(a﹣b)(a4+a3b+a2b2+ab3+b4)= (直接填空);
(2)(a﹣b)(an﹣1+an﹣2b+an﹣3b2…+abn﹣2+bn﹣1)= (直接填空);
(3)利用(2)中得出的结论求62019+62018+…+62+6+1的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按相同路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S和时间t的关系.象回答下列问题:
(1)甲和乙哪一个出发的更早?早出发多长时间?
(2)甲和乙哪一个早到达B城?早多长时间?
(3)乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少?
(4)请你根据图象上的数据,求出乙出发后多长时间追上甲?

-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,某商场搞优惠促销,决定由顾客抽奖确定折扣.某顾客购买甲、乙两种商品,分别抽到七折(按售价的70%销售)和九折(按售价的90%销售),共付款386元,这两种商品原销售价之和为500元.问:这两种商品的原销售价分别为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:
分数段
频数
频率
60≤x<70
30
0.15
70≤x<80
m
0.45
80≤x<90
60
n
90≤x≤100
20
0.1
请根据以上图表提供的信息,解答下列问题:
(1)这次共调查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)如果比赛成绩在80分以上(含80分)可获得奖励,那么获奖概率是多少?

相关试题

