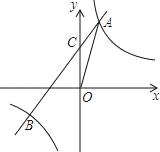
【题目】如图,反比例函数y=![]() 的图象与一次函数y=kx+b的图象交于点A(m,2),点B(﹣2,n ),一次函数图象与y轴的交点为C.
的图象与一次函数y=kx+b的图象交于点A(m,2),点B(﹣2,n ),一次函数图象与y轴的交点为C.
(1)求一次函数解析式;
(2)求C点的坐标;
(3)求△AOB的面积.
参考答案:
【答案】(1)y=x+1;(2)1.5
【解析】试题分析:
(1)把点A、B的坐标代入反比例函数的解析式,求得“m”、“n”的值,再把点A、B的坐标代入![]() 中,列出方程组求得“k”、“b”的值,即可得到一次函数的解析式;
中,列出方程组求得“k”、“b”的值,即可得到一次函数的解析式;
(2)由(1)中所求一次函数的解析式即可求得点C的坐标;
(3)由(2)中所求点C的坐标可得OC的长,作AD⊥y轴于D,作BE⊥y轴于E,由点A、B的坐标可得AD、BE的长,然后由S△AOB=S△AOC+S△BOC即可求得△AOB的面积.
试题解析:
(1)由题意,把A(m,2),B(﹣2,n)代入![]() 中,得
中,得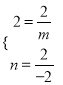 ,解得:
,解得: ![]() ,
,
∴A的坐标为(1,2),B的坐标为(﹣2,﹣1),
将A、B的坐标代入y=kx+b中得: ![]() ,解得:
,解得: ![]() ,
,
∴一次函数的解析式为: ![]() ;
;
(2)∵在![]() 中,当
中,当![]() 时,
时, ![]() ,
,
∴点C的坐标为(0,1);
如图,作AD⊥y轴于D,作BE⊥y轴于E.
∵点C的坐标为(0,1),
∴OC=1,
∵S△A0B=S△A0C+S△BOC,
∴S△A0B=![]() OC×AD+
OC×AD+![]() OC×BE,
OC×BE,
=![]() ×1×(1+2),
×1×(1+2),
=1.5.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,长方形纸片ABCD中,AB=8,将纸片折叠,使顶点B落在边AD上的E点处,折痕的一端G点在边BC上,折痕的另一端F在AD边上且BG=10时.
(1)证明:EF=EG;
(2)求AF的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°,其中正确的结论有( )个
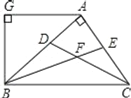
A.1B.2C.3D.4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,已知∠CDB=110°,∠ABD=30°.
(1)请用直尺和圆规在图中直接作出∠A的平分线AE交BD于E;(不写作法,保留作图痕迹)
(2)在(1)的条件下,求出∠AED的度数.

-
科目: 来源: 题型:
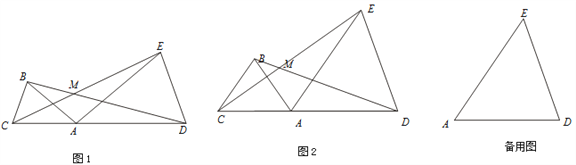
查看答案和解析>>【题目】已知:点C、A、D在同一条直线上,∠ABC=∠ADE=α,线段 BD、CE交于点M.
(1)如图1,若AB=AC,AD=AE
①问线段BD与CE有怎样的数量关系?并说明理由;②求∠BMC的大小(用α表示);
(2)如图2,若AB= BC=kAC,AD =ED=kAE 则线段BD与CE的数量关系为 ,∠BMC= (用α表示);
(3)在(2)的条件下,把△ABC绕点A逆时针旋转180°,在备用图中作出旋转后的图形(要求:尺规作图,不写作法,保留作图痕迹),连接 EC并延长交BD于点M.则∠BMC= (用α表示).
-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下列等式:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4…
利用你的发现的规律解决下列问题
(1)(a﹣b)(a4+a3b+a2b2+ab3+b4)= (直接填空);
(2)(a﹣b)(an﹣1+an﹣2b+an﹣3b2…+abn﹣2+bn﹣1)= (直接填空);
(3)利用(2)中得出的结论求62019+62018+…+62+6+1的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=ax2-2ax+c与y轴交于C点,与x轴交于A、B两点,点A的坐标是(-1,0),O是坐标原点,且OC=3OA.

(1)求抛物线的函数表达式;
(2)直接写出直线BC的函数表达式;
(3)如图1,D为y轴的负半轴上的一点,且OD=2,以OD为边作正方形ODEF.将正方形ODEF以每秒1个单位的速度沿x轴的正方向移动,在运动过程中,设正方形ODEF与△OBC重叠部分的面积为s,运动的时间为t秒(0<t≤2).
求:①s与t之间的函数关系式;
②在运动过程中,s是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由.
(4)如图2,点P(1,k)在直线BC上,点M在x轴上,点N在抛物线上,是否存在以A、M、N、P为顶点的平行四边形?若存在,请直接写出M点坐标;若不存在,请说明理由.
相关试题

