【题目】(13分)如图,在菱形ABCD中,M,N分别是边AB,BC的中点,MP⊥AB交边CD于点P,连接NM,NP.

(1)若∠B=60°,这时点P与点C重合,则∠NMP= 度;
(2)求证:NM=NP;
(3)当△NPC为等腰三角形时,求∠B的度数.
参考答案:
【答案】(1)30;(2)证明见试题解析;(3)108°或90°.
【解析】
试题(1)由直角三角形的中线等于斜边上的一半,即可得出结论;
(2)延长MN交DC的延长线于点E,由四边形ABCD是菱形,得出AB∥DC,从而有∠BMN=∠E,由点N是线段BC的中点,得出BN=CN,得出△MNB≌△ENC,从而有MN=EN,即点N是线段ME的中点,由MP⊥AB交边CD于点P,得出MP⊥DE,从而有∠MPE=90°,即可得出结论;
(3)NC和PN不可能相等,所以只需分①PN=PC,②PC=NC两种情况进行讨论即可.
试题解析:(1)∵MP⊥AB交边CD于点P,∠B=60°,点P与点C重合,∴∠NPM=30°,∠BMP=90°,∵N是BC的中点,∴MN=PN,∴∠NMP=∠NPM=30°;
(2)如图1,延长MN交DC的延长线于点E,∵四边形ABCD是菱形,∴AB∥DC,∴∠BMN=∠E,∵点N是线段BC的中点,∴BN=CN,在△MNB和△ENC中,∵∠BMN=∠E,∠MNB=∠ENC,BN=CN,∴△MNB≌△ENC,∴MN=EN,即点N是线段ME的中点,∵MP⊥AB交边CD于点P,∴MP⊥DE,∴∠MPE=90°,∴PN=MN=![]() ME;
ME;

(3)如图2,∵四边形ABCD是菱形,∴AB=BC,又M,N分别是边AB,BC的中点,∴MB=NB,∴∠BMN=∠BNM,由(2)知:△MNB≌△ENC,∴∠BMN=∠BNM=∠E=∠CNE,又∵PN=MN=NE,∴∠NPE=∠E,设∠BMN=∠BNM=∠E=∠NCE=∠NPE=x°,则∠NCP=2x°,∠NPC=x°,
①若PN=PC,则∠PNC=∠NCP=2x°,在△PNC中,2x+2x+x=180,解得:x=36,∴∠B=∠PNC+∠NPC=2x°+x°=36°×3=108°;
②若PC=NC,则∠PNC=∠NPC=x°,在△PNC中,2x+x+x=180,解得:x=45,∴∠B=∠PNC+∠NPC=x°+x°=45°+45°=90°;
综上所述:∠B=108°或90°.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017甘肃省天水市)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.

-
科目: 来源: 题型:
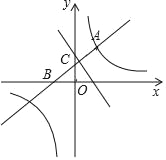
查看答案和解析>>【题目】如图,直线y=x+b与双曲线y=
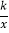 (k是常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.点P在x轴.
(k是常数,k≠0)在第一象限内交于点A(1,2),且与x轴、y轴分别交于B,C两点.点P在x轴.(1)求直线和双曲线的解析式;
(2)若△BCP的面积等于2,求P点的坐标;
(3)求PA+PC的最短距离.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,CF⊥AB于点F,BE⊥AC于点E,M为BC的中点连接ME、MF、EF.
(1) 求证:△MEF是等腰三角形;
(2) 若∠A=
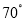 ,∠ABC=50°,求∠EMF的度数.
,∠ABC=50°,求∠EMF的度数.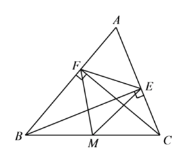
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为
 ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为

D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的直径,点F、C是⊙O上两点,且
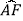 =
= 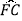 =
=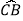 ,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2
,连接AC、AF,过点C作CD⊥AF,交AF的延长线于点D,垂足为D,若CD=2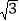 ,则⊙O的半径为( )
,则⊙O的半径为( )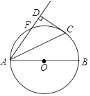
A. 2
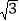 B. 4
B. 4 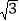 C. 2 D. 4
C. 2 D. 4 -
科目: 来源: 题型:
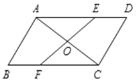
查看答案和解析>>【题目】如图,AC是平行四边形ABCD的一条对角线,过AC中点O的直线分别交 AD,BC 于点 E,F.
(1)求证:四边形AECF是平行四边形;
(2)当 EF 与 AC 满足什么条件时,四边形 AECF 是菱形?并说明理由.
相关试题

