【题目】某环卫公司承包了市区两个片区道路的清扫任务,需要购买某厂家A,B两种型号的马路清扫车,购买5辆A型马路清扫车和6辆B型马路清扫车共需171万元;购买3辆A型马路清扫车和12辆B型马路清扫车共需237万元.
(1)求这两种马路清扫车的单价;
(2)恰逢该厂举行30周年庆,决定对这两种马路清扫车开展促销活动,具体方案如下:购买A型马路清扫车按原价的八折销售,购买B型马上清扫车不超过10辆时按原价销售,超过10辆的部分按原价的七折销售.设购买x辆A种马路清扫车需要y1元,购买x(x>0)个B型马路清扫车需要y2元,分别求出y1,y2关于x的函数关系式;
(3)若该公司承包的道路清扫面积为118000m2,每辆A型马路清扫车每天清扫5000m2,每辆B型马路清扫车每天清扫6000m2,公司准备购买20辆马路清扫车,且B型马路清扫车的数量大于10.请你帮该公司设计出最省钱的购买方案.请说明理由.
参考答案:
【答案】(1)A型马路清扫车的单价为15万元,B型马路清扫车的单价为16万元;(2)y1=12x,当0<x≤10时,y2=16x;当x>10时,y2=11.2x+48;(3)该公司购买A型马路清扫车2辆,购买B型马路清扫车18辆时最省钱,最低费用为273.6万元.
【解析】
(1)设A型马路清扫车的单价为a万元,B型马路清扫车的单价为b万元,根据“购买5辆A型马路清扫车和6辆B型马路清扫车共需171万元;购买3辆A型马路清扫车和12辆B型马路清扫车共需237万元”即可得出关于a、b的二元一次方程组,解方程组即可得出结论;
(2)根据“A型马路清扫车按原价的八折销售,购买B型马上清扫车不超过10辆时按原价销售,超过10辆的部分按原价的七折销售”,即可得出y1、y2关于x的函数关系式;
(3)设该公司购买B型马路清扫车m辆,则购买A型马路清扫车(20m)辆,根据题意求出m的取值范围,即可解答.
(1)设A型马路清扫车的单价为a万元,B型马路清扫车的单价为b万元,
则由题意可知:![]() ,解得
,解得![]() ,
,
答:A型马路清扫车的单价为15万元,B型马路清扫车的单价为16万元;
(2)由题意可知:y1=0.8×15x,即y1=12x,
当0<x≤10时,y2=16x;
当x>10时,y2=16×10+16(x﹣10)×0.7,即y2=11.2x+48.
∴y2=![]() ;
;
(3)设该公司购买B型马路清扫车m辆,则购买A型马路清扫车(20﹣m)辆,
根据题意得,![]() ,
,
解得m≥18,
∵A型马路清扫车的单价比B型马路清扫车的单价便宜,
∴m=18时,该公司最省钱,此时购买总费用为:15×0.8×(20﹣18)+16×10+16×0.7×(18﹣10)=273.6(万元).
即该公司购买A型马路清扫车2辆,购买B型马路清扫车18辆时最省钱,最低费用为273.6万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,E、F分别是BC、CD上的点,且∠EAF=45°,AE、AF分别交BD于M、N,连按EN、EF,有以下结论:
①△ABM∽△NEM;②△AEN是等腰直角三角形;③当AE=AF时,
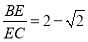 ;④BE+DF=EF;⑤若点F是DC的中点,则CE
;④BE+DF=EF;⑤若点F是DC的中点,则CE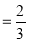 CB.
CB.其中正确的个数是( )

A.2B.3C.4D.5
-
科目: 来源: 题型:
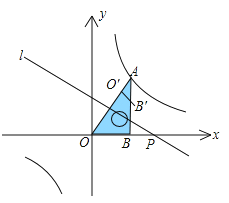
查看答案和解析>>【题目】如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOB=60°,点A在第一象限,过点A的双曲线为
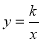 .在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是OB.
.在x轴上取一点P,过点P作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是OB.(1)当点O与点A重合时,点P的坐标是 ;
(2)设P(t,0),当OB与双曲线有交点时,t的取值范围是 .
-
科目: 来源: 题型:
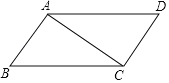
查看答案和解析>>【题目】如图,已知四边形ABCD是平行四边形.
(1)用直尺和圆规作出对角线AC的垂直平分线,分别交AD,BC于E,F;(保留作图痕迹,不写作法)
(2)在(1)作出的图形中,连接CE,AF,若AB=4,BC=8,且AB⊥AC,求四边形AECF的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】2018年平昌冬奥会在2月9日到25日在韩国平昌郡举行,为了调查中学生对冬奥会比赛项目的了解程度,某中学在学生中做了一次抽样调查,调查结果共分为四个等级:A、非常了解B、比较了解C、基本了解D、不了解.根据调查统计结果,绘制了如图所示的不完整的三种统计图表.
对冬奥会了解程度的统计表
对冬奥会的了解程度
百分比
A非常了解
10%
B比较了解
15%
C基本了解
35%
D不了解
n%
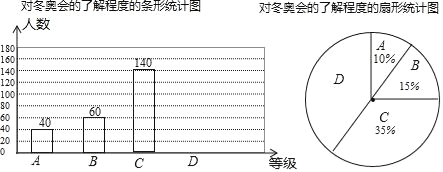
(1)n= ;
(2)扇形统计图中,D部分扇形所对应的圆心角是 ;
(3)请补全条形统计图;
(4)根据调查结果,学校准备开展冬奥会的知识竞赛,某班要从“非常了解”程度的小明和小刚中选一人参加,现设计了如下游戏来确定谁参赛,具体规则是:把四个完全相同的乒乓球标上数字1,2,3,4然后放到一个不透明的袋中,一个人先从袋中摸出一个球,另一人再从剩下的三个球中随机摸出一个球,若摸出的两个球上的数字和为偶数,则小明去,否则小刚去,请用画树状图或列表的方法说明这个游戏是否公平.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的对角线AC和BD交于点O,分别过点C、D作CE∥BD,DE∥AC,CE和DE交于点E.
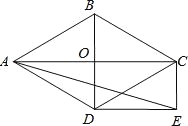
(1)求证:四边形ODEC是矩形;
(2)当∠ADB=60°,AD=2
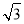 时,求sin∠AED的值,求∠EAD的正切值.
时,求sin∠AED的值,求∠EAD的正切值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;
(2)若
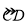 的长为
的长为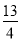 π,求“回旋角”∠CPD的度数;
π,求“回旋角”∠CPD的度数;(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13
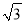 ,直接写出AP的长.
,直接写出AP的长.
相关试题

