Question

【题目】二次函数y=ax2+bx+1（a≠0）的图象的顶点在第一象限，且过点（-1，0）．设t=a+b+1，则t值的变化范围是（ ）

A. 0＜t＜1 B. 0＜t＜2 C. 1＜t＜2 D. -1＜t＜1

Answer 1

【答案】B

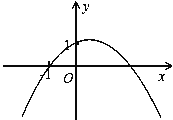
【解析】试题分析：此题是压轴题．考查了点与函数的关系，解题的关键是画草图，利用数形结合思想解题．由二次函数的解析式可知，当x=1时，所对应的函数值y=t=a+b+1．把点（﹣1，0）代入y=ax2+bx+1，a﹣b+1=0，然后根据顶点在第一象限，可以画出草图并判断出a与b的符号，进而求出t=a+b+1的变化范围．

解：∵二次函数y=ax2+bx+1的顶点在第一象限，

且经过点（﹣1，0），

∴易得：a﹣b+1=0，a＜0，b＞0，

由a=b﹣1＜0得到b＜1，结合上面b＞0，所以0＜b＜1①，

由b=a+1＞0得到a＞﹣1，结合上面a＜0，所以﹣1＜a＜0②，

∴由①+②得：﹣1＜a+b＜1，

在不等式两边同时加1得0＜a+b+1＜2，

∵a+b+1=t代入得0＜t＜2，

∴0＜t＜2．

故选：B．